
【题目】已知函数f(x)=x2-ax+2lnx,a∈R.
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线垂直于直线y=x,求函数f(x)的单调区间;
(Ⅱ)若x>1时,f(x)>0恒成立,求实数a的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)(-∞,1].
【解析】试题分析:(I)求出函数的导数,求得切线的斜率,由题意可得斜率为-1,可得![]() ,求出导数,令导数大于0,可得增区间,令导数小于0,可得减区间;
,求出导数,令导数大于0,可得增区间,令导数小于0,可得减区间;
(Ⅱ)运用参数分离,可得![]() 在
在![]() 时恒成立,令
时恒成立,令![]() 求得导数,判断函数的单调性,运用单调性即可求得
求得导数,判断函数的单调性,运用单调性即可求得![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)f(x)定义域为(0,+∞),f′(x)=2x-a+![]() ,
,
f′(1)=4-a=-1 ,a=5,
f(x)=x2-5x+2lnx,f′(x)=2x-5+![]() =
=![]() ,
,
当x>2或0<x<![]() 时,f′(x)>0,当
时,f′(x)>0,当![]() <x<2时,f′(x)<0,
<x<2时,f′(x)<0,
故f(x)的单调递增区间为(0, ![]() ),(2,+∞),单调递减区间为(
),(2,+∞),单调递减区间为(![]() ,2).
,2).
(Ⅱ)由f(x)>0,得a<![]() 在x>1时恒成立,
在x>1时恒成立,
令g(x)=![]() ,g′(x)=
,g′(x)=![]()
令h(x)=x2+2-2lnx,h′(x)=2x-![]() >0在x>1时成立,
>0在x>1时成立,
所以h(x)在(1,+∞)为增函数,h(x)>h(1)=3>0 .
故g′(x)>0,故g(x)在(1,+∞)为增函数.g(x)>g(1)=1,
所以a≤1,即实数a的取值范围为(-∞,1].


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
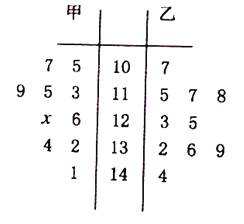
【题目】为了减少雾霾,还城市一片蓝天,某市政府于12月4日到12月31日在主城区实行车辆限号出行政策,鼓励民众不开车低碳出行,某甲乙两个单位各有200名员工,为了了解员工低碳出行的情况,统计了12月5日到12月14日共10天的低碳出行的人数,画出茎叶图如下:
(1)若甲单位数据的平均数是122,求![]() ;
;
(2)现从如图的数据中任取4天的数据(甲、乙两单位中各取2天),记其中甲、乙两单位员工低碳出行人数不低于130人的天数为![]() ,
, ![]() ,令
,令![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
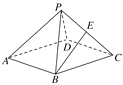
A. BE∥平面PAD,且BE到平面PAD的距离为![]()
B. BE∥平面PAD,且BE到平面PAD的距离为![]()
C. BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D. BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为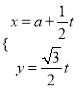
![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于A,B两点,当
交于A,B两点,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·河西五市二联)下列说法正确的是( )
A. 命题“x∈R,ex>0”的否定是“x∈R,ex>0”
B. 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题
C. “x2+2x≥ax在x∈[1,2]上恒成立”“(x2+2x)min≥(ax)min在x∈[1,2]上恒成立”
D. 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)过点(1,
(a>b>0)过点(1, ![]() ),且离心率e=
),且离心率e=![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),椭圆的右顶点为D,且满足![]() ·
·![]() =0,试判断直线l是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
=0,试判断直线l是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com