
【题目】已知函数![]() ,
,![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() ,求
,求![]() 的单调区间;并证明:当
的单调区间;并证明:当![]() 时,
时,![]() ;
;
(3)证明:当![]() 时,函数
时,函数 有最小值,设
有最小值,设![]() 最小值为
最小值为![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2)![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;证明见解析;(3)证明见解析;
;证明见解析;(3)证明见解析;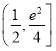 .
.
【解析】
(1)由导数的几何意义可得切线斜率为1,利用点斜式即可得解;
(2)由题意![]() ,求导后可得
,求导后可得![]() ,即可得
,即可得![]() 的单调区间;由
的单调区间;由![]() 时,
时,![]() 即
即![]() ,即可得证;
,即可得证;
(3)求出函数![]() 的导数,令
的导数,令![]() ,由(2)知
,由(2)知![]() 的单调性,可得存在唯一实数
的单调性,可得存在唯一实数![]() 使得
使得![]() ,则
,则![]() ,令
,令![]() ,求导后即可得解.
,求导后即可得解.
(1)![]()
![]() ,
,![]()
 ,
,![]()
![]() ,
,
故所求直线方程为![]() 即
即![]() ;
;
(2)由题意![]() ,
,
则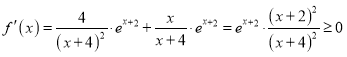 ,
,
![]()
![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ;
;
![]() 当
当![]() 时,
时,![]() 即
即![]() ,
,
由![]() 可得
可得![]() 即
即![]() ,
,
![]()
![]() ,得证.
,得证.
(3)由题意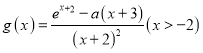 ,
,
则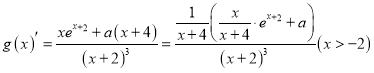 ,
,
设![]() ,
,
由(2)知,![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,![]() 存在唯一实数
存在唯一实数![]() 使得
使得![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递增;
单调递增;
![]()
![]() 在
在![]() 上有最小值
上有最小值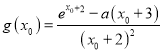 即
即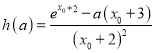 ,
,
又![]() 即
即![]() ,
,
![]()
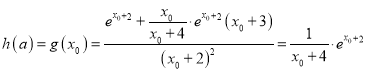 ,
,
令![]() ,
,
则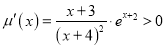 ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
![]()
![]() 即
即![]() ,
,
![]() 函数
函数![]() 的值域为
的值域为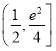 .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】袋中共有8个乒乓球,其中有5个白球,3个红球,这些乒乓球除颜色外完全相同.从袋中随机取出一球,如果取出红球,则把它放回袋中;如果取出白球,则该白球不再放回,并且另补一个红球放入袋中,重复上述过程![]() 次后,袋中红球的个数记为
次后,袋中红球的个数记为![]() .
.
(I)求随机变量![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
(Ⅱ)求随机变量![]() 的数学期望
的数学期望![]() 关于
关于![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数为( )
①两个有共同始点且相等的向量,其终点可能不同;
②若非零向量![]() 与
与![]() 共线,则
共线,则![]() 、
、![]() 、
、![]() 、
、![]() 四点共线;
四点共线;
③若非零向量![]() 与
与![]() 共线,则
共线,则![]() ;
;
④四边形![]() 是平行四边形,则必有
是平行四边形,则必有![]() ;
;
⑤![]() ,则
,则![]() 、
、![]() 方向相同或相反.
方向相同或相反.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个定点![]() ,
,![]() , 动点
, 动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() :
:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 、
、![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率;
的斜率;
(3)若![]() ,
,![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作曲线
作曲线![]() 的两条切线
的两条切线![]() 、
、![]() ,切点为
,切点为![]() 、
、![]() ,探究:直线
,探究:直线![]() 是否过定点,若存在定点请写出坐标,若不存在则说明理由.
是否过定点,若存在定点请写出坐标,若不存在则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com