
图1
活动:教师引导学生回顾,向量具有二重性,一方面具有“形”的特点,因此有了几何运算;另一方面又具有一套优良的代数运算性质,因此又有了代数运算.对于这两种运算,前者难度大,灵活多变,对学生来说是个难点,后者学生感到熟悉,易于掌握,但应让学生明了,这两种方法都要掌握好,近几年高考题的解答都是以两种解法给出.本题给出的是三角形,对于某些几何命题的抽象的证明,自然可以转化为向量的几何运算问题来解决,请同学们在探究中要注意仔细体会,领悟其实质.教学中,教师要放手大胆地让学生自己去探究,鼓励学生从不同的角度去观察、去发现.真正做到一题多用,一题多变,串联知识,串联方法,使学生在探究过程中掌握孤零知识,提高思维能力,提高复习效率.
证法一:由题意,得a+b+c=0,∴c=-(a+b).
又∵b·c=c·a,∴c·(a-b)=0.
∴-a2+b2=0.∴|a|2=|b|2,即|a|=|b|.
同理可得|c|=|b|,∴|a|=|b|=|c|.
∴△ABC为正三角形.
证法二:由题意得a+b+c=0,∴a=-b-c,b=-a-c.
∴a2=b2+c2+2b·c,b2=a2+c2+2a·c.
而b·c=c·a(已知),
∴a2-b2=b2-a2.
∴a2=b2.∴|a|2=|b|2.
∴|a|=|b|.
同理可得|c|=|b|,∴|a|=|b|=|c|.
∴△ABC为正三角形.

图2
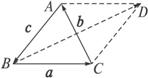
证法三:如图2,以AB,BC为邻边作![]() ABCD,则
ABCD,则![]() =a,
=a,![]() =
=![]() -
-![]() ,
,
∴![]() =a-c.
=a-c.
又∵a·b=b·c,∴b·(a-c)=0.
∴b·![]() =0.∴b⊥
=0.∴b⊥![]() .
.
∴![]() ABCD为菱形.∴AB=BC.同理可得BC=AC,
ABCD为菱形.∴AB=BC.同理可得BC=AC,
∴△ABC为正三角形.
证法四:取![]() 的中点E,连接AE,则
的中点E,连接AE,则
![]() =
=![]() (
(![]() +
+![]() )=
)=![]() (c-b),
(c-b),
∴![]() ·a=
·a=![]() (c-b)·a=0.
(c-b)·a=0.
∴![]() ⊥a.∴AB=AC.
⊥a.∴AB=AC.
同理可得BC=AC,
∴△ABC为正三角形.
点评:本题给出了四种证法,教师要善于引导学生进行一题多解,这是一种很有效的办法.数学教学中,一题多解训练是培养学生思维灵活的一种良好手段.通过一题多解的训练能沟通知识之间的内在联系,提高学生应用所学的基础知识与基本技能解决实际问题的能力,逐步学会举一反三的本领,在教材安排的例题中,有相当一部分题目存在一题多解的情况,教师要引导学生善于挖掘.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
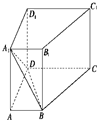 如图,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.
如图,已知在直四棱柱ABCD-A1B1C1D1中,AD⊥DC,AB∥DC,DC=DD1=2AD=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:
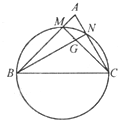 (2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若
(2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若| BM |
| BC |
| CN |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•杭州二模)如图,已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=
(2013•杭州二模)如图,已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
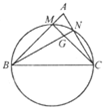 如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若
如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若| BM |
| BC |
| CN |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
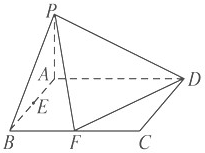 如图,已知在四棱锥PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
如图,已知在四棱锥PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com