
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЪЧЮвЙњЙХДњжјУћЪ§бЇОЕфЃЌЦфжаЖдЙДЙЩЖЈРэЕФТлЪіЃЌБШЮїЗНдчвЛЧЇЖрФъЃЌЦфжагаетбљвЛИіЮЪЬтЃКЁАНёгадВВФТёдкБкжаЃЌВЛжЊДѓаЁЃЛвдОтОтжЎЃЌЩювЛДчЃЌОтЕРГЄвЛГпЃЌЮЪОЖМИКЮЃПЁБЦфвтЮЊЃКНёгавЛдВжљаЮФОВФЃЌТёдкЧНБкжаЃЌВЛжЊЦфДѓаЁЃЌгУОтШЅОтИУВФСЯЃЌОтПкЩю1ДчЃЌОтЕРГЄ1ГпЃЌЮЪетПщдВжљаЮФОСЯЕФжБОЖЪЧЖрЩйЃПГЄЮЊ0.5еЩЕФдВжљаЮФОВФВПЗжЯтЧЖдкЧНЬхжаЃЌНиУцЭМШчЭМЫљЪОЃЈвѕгАВПЗжЮЊЯтЧЖдкЧНЬхФкЕФВПЗжЃЉ.МКжЊЯв![]() ГпЃЌЙаЮИп
ГпЃЌЙаЮИп![]() ДчЃЌЙРЫуИУФОВФЯтЧЖЧНФкВПЗжЕФЬхЛ§дМЮЊЃЈ ЃЉЃЈзЂЃКвЛеЩ=10Гп=100ДчЃЌ
ДчЃЌЙРЫуИУФОВФЯтЧЖЧНФкВПЗжЕФЬхЛ§дМЮЊЃЈ ЃЉЃЈзЂЃКвЛеЩ=10Гп=100ДчЃЌ![]() ЃЉ
ЃЉ
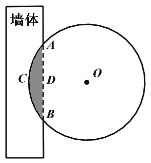
A.300СЂЗНДчB.305.6СЂЗНДчC.310СЂЗНДчD.316.6СЂЗНДч
 ЖсЙкН№ОэШЋФмСЗПМЯЕСаД№АИ
ЖсЙкН№ОэШЋФмСЗПМЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДќжаЙВга8ИіЧђЃЌЦфжага3ИіАзЧђЃЌ5ИіКкЧђЃЌетаЉЧђГ§беЩЋЭтЭъШЋЯрЭЌЃЎДгДќжаЫцЛњШЁГівЛЧђЃЌШчЙћШЁГіАзЧђЃЌдђАбЫќЗХЛиДќжаЃЛШчЙћШЁГіКкЧђЃЌдђИУКкЧђВЛдйЗХЛиЃЌВЂЧвСэВЙвЛИіАзЧђЗХШыДќжаЃЎжиИДЩЯЪіЙ§ГЬ![]() ДЮКѓЃЌДќжаАзЧђЕФИіЪ§МЧЮЊ
ДЮКѓЃЌДќжаАзЧђЕФИіЪ§МЧЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЫцЛњБфСП![]() ЕФИХТЪЗжВММАЪ§бЇЦкЭћ
ЕФИХТЪЗжВММАЪ§бЇЦкЭћ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЫцЛњБфСП![]() ЕФЪ§бЇЦкЭћ
ЕФЪ§бЇЦкЭћ![]() Йигк
Йигк![]() ЕФБэДяЪНЃЎ
ЕФБэДяЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫуГяЪЧдкжщЫуЗЂУївдЧАЮвЙњЖРДДВЂЧвгааЇЕФМЦЫуЙЄОпЃЌЮЊЮвЙњЙХДњЪ§бЇЕФЗЂеЙзіГіСЫКмДѓЙБЯз.дкЫуГяМЧЪ§ЗЈжаЃЌвдЁАзнЪНЁБКЭЁАКсЪНЁБСНжжЗНЪНРДБэЪОЪ§зжЃЌШчЯТБэЃК
Ъ§зжаЮЪН |
|
|
|
|
|
|
|
|
|
знЪН |
|
|
|
|
|
|
|
|
|
КсЪН |
|
|
|
|
|
|
|
|
|
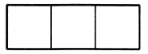
БэЪОЖрЮЛЪ§ЪБЃЌИіЮЛгУзнЪНЃЌЪЎЮЛгУКсЪНЃЌАйЮЛгУзнЪНЃЌЧЇЮЛгУКсЪНЃЌвдДЫРрЭЦЃЌгіСудђжУПеЃЌШчЭМЫљЪО.ШчЙћАб![]() ИљЫуГявдЪЪЕБЕФЗНЪНШЋВПЗХШыЯТУцЕФБэИёжаЃЌФЧУДПЩвдБэЪОЕФШ§ЮЛЪ§ЕФИіЪ§ЮЊ______.
ИљЫуГявдЪЪЕБЕФЗНЪНШЋВПЗХШыЯТУцЕФБэИёжаЃЌФЧУДПЩвдБэЪОЕФШ§ЮЛЪ§ЕФИіЪ§ЮЊ______.
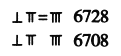
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇФГЩчЭХЮЊбаОПИпШ§бЇЩњПЮЯТзъбаЪ§бЇЪБМфгыЪ§бЇПМЪджаЕФНтД№ЬтЕУЗжЕФЙиЯЕЃЌЫцЛњЕїВщСЫФГжабЇИпШ§ФГАр![]() УћбЇЩњУПжмПЮЯТзъбаЪ§бЇЪБМф
УћбЇЩњУПжмПЮЯТзъбаЪ§бЇЪБМф![]() (ЕЅЮЛЃКаЁЪБ)гыИпШ§ЯТбЇЦкЦкжаПМЪдЪ§бЇНтД№ЬтЕУЗж
(ЕЅЮЛЃКаЁЪБ)гыИпШ§ЯТбЇЦкЦкжаПМЪдЪ§бЇНтД№ЬтЕУЗж![]() ЃЌЪ§ОнШчЯТБэЃК
ЃЌЪ§ОнШчЯТБэЃК
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
ЃЈ1ЃЉИљОнЩЯЪіЪ§ОнЃЌЧѓГіЪ§бЇПМЪджаЕФНтД№ЬтЕУЗж![]() гыИУбЇЩњПЮЯТзъбаЪ§бЇЪБМф
гыИУбЇЩњПЮЯТзъбаЪ§бЇЪБМф![]() ЕФЯпадЛиЙщЗНГЬЃЌВЂдЄВтФГбЇЩњУПжмПЮЯТзъбаЪ§бЇЪБМфЮЊ
ЕФЯпадЛиЙщЗНГЬЃЌВЂдЄВтФГбЇЩњУПжмПЮЯТзъбаЪ§бЇЪБМфЮЊ![]() аЁЪБЦфЪ§бЇПМЪджаЕФНтД№ЬтЕУЗжЃЛ
аЁЪБЦфЪ§бЇПМЪджаЕФНтД№ЬтЕУЗжЃЛ
ЃЈ2ЃЉДгет![]() ШЫжаШЮбЁ
ШЫжаШЮбЁ![]() ШЫЃЌЧѓ
ШЫЃЌЧѓ![]() ШЫжажСЩйга
ШЫжажСЩйга![]() ШЫПЮЯТзъбаЪ§бЇЪБМфВЛЕЭгк
ШЫПЮЯТзъбаЪ§бЇЪБМфВЛЕЭгк![]() аЁЪБЕФИХТЪ.
аЁЪБЕФИХТЪ.
ВЮПМЙЋЪНЃК![]() ЃЌЦфжа
ЃЌЦфжа ЃЌ
ЃЌ![]() ЃЛВЮПМЪ§ОнЃК
ЃЛВЮПМЪ§ОнЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЧѓЧњЯп![]() Й§дЕуЕФЧаЯпЗНГЬЃЛ
Й§дЕуЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉЩш![]() ЃЌШєКЏЪ§
ЃЌШєКЏЪ§![]() ЕФЕМКЏЪ§
ЕФЕМКЏЪ§![]() ДцдкСНИіВЛЭЌЕФСуЕу
ДцдкСНИіВЛЭЌЕФСуЕу![]() ЃЌ
ЃЌ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФЗЖЮЇЃК
ЕФЗЖЮЇЃК
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТжЄУїЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌжБЯп
ЮЊВЮЪ§ЃЉЃЌжБЯп![]() ЃЈtЮЊВЮЪ§ЃЉЃЌвддЕуOЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕ
ЃЈtЮЊВЮЪ§ЃЉЃЌвддЕуOЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕ
ЃЈ1ЃЉЧѓЧњЯпCгыжБЯпlЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпlгыЧњЯпCЯрНЛЃЌНЛЕуЮЊ![]() ЃЌжБЯпгыxжсНЛгкQЕуЃЌЧѓ
ЃЌжБЯпгыxжсНЛгкQЕуЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфЕМКЏЪ§ЮЊ
ЃЌЦфЕМКЏЪ§ЮЊ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЃЌЖдШЮвт
ЃЌЖдШЮвт![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂ.
КуГЩСЂ.
ЃЈ1ЃЉЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпC1ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈtЮЊВЮЪ§ЃЌ0ЃМІСЃМІаЃЉЃЌЧњЯпC2ЕФВЮЪ§ЗНГЬЮЊ
ЃЈtЮЊВЮЪ§ЃЌ0ЃМІСЃМІаЃЉЃЌЧњЯпC2ЕФВЮЪ§ЗНГЬЮЊ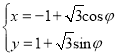 ЃЈІеЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕ.
ЃЈІеЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕ.
ЃЈ1ЃЉЧѓЧњЯпC2ЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшЧњЯпC1гыЧњЯпC2ЕФНЛЕуЗжБ№ЮЊAЃЌBЃЌMЃЈЉ2ЃЌ0ЃЉЃЌЧѓ|MA|2+|MB|2ЕФзюДѓжЕМАДЫЪБжБЯпC1ЕФЧуаБНЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЭЌбЇЖдРтГЄЮЊ2ЕФе§ЗНЬхЕФаджЪНјаабаОПЃЌЕУЕНСЫШчЯТНсТлЃКЂй12ЬѕРтжаПЩЙЙГЩ16ЖдвьУцжБЯпЃЛЂкЙ§е§ЗНЬхЕФвЛИіЖЅЕуЕФНиУцПЩФмЪЧШ§НЧаЮЁЂЫФБпаЮЁЂЮхБпаЮЁЂСљБпаЮЃЛЂлвде§ЗНЬхИїБэУцжааФЮЊЖЅЕуЕФе§АЫУцЬхЕФБэУцЛ§ЪЧ![]() ЃЛЂмгые§ЗНЬхИїРтЯрЧаЕФЧђЕФЬхЛ§ЪЧЃК
ЃЛЂмгые§ЗНЬхИїРтЯрЧаЕФЧђЕФЬхЛ§ЪЧЃК![]() .Цфжае§ШЗЕФађКХЪЧ______.
.Цфжае§ШЗЕФађКХЪЧ______.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com