
����Ŀ��ij����Ϊ�˼��һ����ˮ�ߵ�����������Ӹ���ˮ���������ȡ40����Ʒ��������Щ��Ʒ����������λ���ˣ���������õ����µ�Ƶ�ʷֲ�ֱ��ͼ�����������ķ�������ֱ�Ϊ��490��495]����495��500]����500��505]����505��510]����510��515]�� ��I��������40����Ʒ����ȡ��������XΪ��������505�˵IJ�Ʒ���������������X�ķֲ��У�
���������������ֲ����ƿ�������ֲ����ִӸ���ˮ������ȡ5����Ʒ����ǡ��������Ʒ����������505�˵ĸ��ʣ�
���𰸡��⣺��I������Ƶ�ʷֲ�ֱ��ͼ��֪����������505�˵IJ�Ʒ����Ϊ[��0.001+0.005����5]��40=12�� ��������������X�����п���ȡֵΪ 0��1��2![]() =
= ![]() ��
�� ![]() ��
�� ![]() ��
��
���������X�ķֲ���Ϊ
X | 0 | 1 | 2 |
P |
|
|
|
����������ø���ˮ���ϲ�Ʒ����������505�˵ĸ���Ϊ0.3
��YΪ����ˮ������ȡ5����Ʒ��������505�˵IJ�Ʒ��������Y��B��5��0.3����
���������ΪP��Y=2��= ![]()
���������� I������Ƶ�ʷֲ�ֱ��ͼ�����������505�˵IJ�Ʒ�������Ƴ��������X�����п���ȡֵΪ 0��1��2 ������ʣ��õ��������X�ķֲ��У������������ˮ���ϲ�Ʒ����������505�˵ĸ���Ϊ0.3���Ƴ�Y��B��5��0.3����Ȼ�����������ʣ�
�����㾫����������Ҫ��������ɢ�������������ֲ��е����֪ʶ�㣬��Ҫ�������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в�����ȷ�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ԲC1�� ![]() ��a��b��0������ΪF1����1��0�����ҵ�P��0��1����C1�ϣ�
��a��b��0������ΪF1����1��0�����ҵ�P��0��1����C1�ϣ�
��1������ԲC1�ķ��̣�
��2����ֱ��lͬʱ����ԲC1��������C2��y2=4x���У���ֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��8��8�����ҹ���ʮ��ȫ�����գ��������ǣ���ʱ��ȫ������������ij��Ϊ�˽�ȫ��������������ijС�������г�ȡ��40�ˣ������ǵ�����ֳ�7�Σ�[10��20����[20��30����[30��40����[40��50����[50��60����[60��70����[70��80]��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
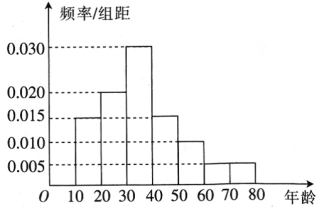
��1��������40�������ƽ��������λ���Ĺ���ֵ��
��2����i������������������[50��70���ľ�������ȡ2�����ͽ�����������2����������1�����䲻����60��ĸ��ʣ�
��������֪��С��������[10��80]�ڵ�������Ϊ2000����18�����ϣ���18�꣩Ϊ�����ˣ��Թ��Ƹ�С�����䲻����80��ij�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵ����һ�־��ܵ��������Ĺ̶��ɱ�Ϊ20000Ԫ��ÿ����һ̨����������Ͷ��100Ԫ����֪���������㺯���� ����x���������²���.
����x���������²���.
��1���������ʾΪ�²����ĺ�����
��2�����²���Ϊ��ֵʱ����˾�������������������Ƕ���Ԫ����������=�ܳɱ�+����.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
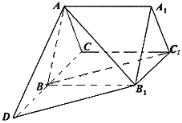
����Ŀ����ͼ����������![]() �ĵ���߳�Ϊ3������
�ĵ���߳�Ϊ3������![]() ��D��CB�ӳ�����һ�㣬��
��D��CB�ӳ�����һ�㣬��![]() ��
��
![]() ������
������![]() ������ֵ��
������ֵ��
![]() ������
������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() ��Բ
��Բ![]() ����ֱ��
����ֱ��![]() �Գƣ�Բ���ڵڶ����ޣ��뾶Ϊ
�Գƣ�Բ���ڵڶ����ޣ��뾶Ϊ![]() .
.
��1����Բ![]() �ķ��̣�
�ķ��̣�
��2��ֱ��![]() ��Բ
��Բ![]() ���У�����
���У�����![]() �ᡢ
�ᡢ![]() ���ϵĽؾ���ȣ���ֱ��
���ϵĽؾ���ȣ���ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x������f����x��=f��x������f��x+2��=f��x��+f��2������x��[0��1]ʱ��f��x��=x����ô������[��1��3]�ڣ�����x�ķ���f��x��=kx+k+1��k��R����k�٩�1ǡ��4����ͬ�ĸ�����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC��Բ��C��ֱ��![]() �ϣ�
�ϣ�
![]() ��ԲC��y��ĸ��������У��Ҹ�Բ��x�����õ��ҳ�Ϊ
��ԲC��y��ĸ��������У��Ҹ�Բ��x�����õ��ҳ�Ϊ![]() ����ԲC�ı����̣�
����ԲC�ı����̣�
![]() ��֪��
��֪��![]() ��ԲC�İ뾶Ϊ3����Բ��C�ڵ�һ���ޣ���ԲC�ϴ��ڵ�M��ʹ
��ԲC�İ뾶Ϊ3����Բ��C�ڵ�һ���ޣ���ԲC�ϴ��ڵ�M��ʹ![]() Ϊ����ԭ��
Ϊ����ԭ��![]() ����Բ��C���������ȡֵ��Χ��
����Բ��C���������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com