
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q.
,长轴长为4,过椭圆的左顶点A作直线l,分别交椭圆和圆x2+y2=a2于相异两点P,Q. 
(1)若直线l的斜率为 ![]() ,求
,求 ![]() 的值;
的值;
(2)若 ![]() =λ
=λ ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
【答案】
(1)解:由条件可得,2a=4,e= ![]() =
= ![]() ,a2﹣b2=c2,
,a2﹣b2=c2,
解得a=2,b=c= ![]() ,
,
可得椭圆的方程为 ![]() ,圆的方程为x2+y2=4;
,圆的方程为x2+y2=4;
(方法一)直线l的方程为 ![]() ,由
,由 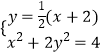 得:3x2+4x﹣4=0,
得:3x2+4x﹣4=0,
解得 ![]() ,所以
,所以 ![]() ;
;
所以 ![]() ,又因为原点O到直线l的距离
,又因为原点O到直线l的距离 ![]() ,
,
所以 ![]() ,
,
所以 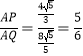 ;
;
(方法二)由 ![]() 得3y2﹣4y=0,所以yP=
得3y2﹣4y=0,所以yP= ![]() ,
,
由 ![]() 可得5y2﹣8y=0,解得yQ=
可得5y2﹣8y=0,解得yQ= ![]() ,
,
所以 ![]() =
= ![]() =
= ![]() ×
× ![]() =
= ![]()
(2)解:(方法一)若 ![]() ,则λ=
,则λ= ![]() ﹣1,
﹣1,
设直线l:y=k(x+2),由 ![]() 得,(2k2+1)x2+8k2﹣4=0,
得,(2k2+1)x2+8k2﹣4=0,
即(x+2)[(2k2+1)x+(4k2﹣2)]=0,
所以 ![]() ,得
,得 ![]() ;
;
所以 ![]() ,
,
即 ![]() ,同理Q(
,同理Q( ![]() ,
, ![]() ),
), ![]() ,
,
即有λ= ![]() ﹣1=1﹣
﹣1=1﹣ ![]() ,
,
由k2>0,可得0<k2<1.
(方法二)由方法一可得,λ= ![]() ﹣1=
﹣1= ![]() ﹣1=
﹣1= ![]() ﹣1=1﹣
﹣1=1﹣ ![]() ,
,
由题意:k2>0,所以0<λ<1
【解析】(1)由题意可得a=2,运用离心率公式和a,b,c的关系可得b,c,进而得到椭圆方程和圆的方程,设出直线l的方程代入椭圆方程,求得弦长AP,运用圆的弦长公式可AQ,进而所求之比;或联立直线的方程和椭圆方程(或圆的方程)求得P,Q的纵坐标,即可得到所求之比;(2)若 ![]() ,则
,则 ![]() ,设直线l:y=k(x+2),代入椭圆方程,求得交点,以及弦长AP,代入圆方程可得交点,可得弦长AQ,可得实数λ的式子,运用不等式的性质即可得到所求范围;或将直线方程代入椭圆方程(圆方程)求得P,Q的纵坐标,由坐标之比,结合不等式的性质,即可得到所求范围.
,设直线l:y=k(x+2),代入椭圆方程,求得交点,以及弦长AP,代入圆方程可得交点,可得弦长AQ,可得实数λ的式子,运用不等式的性质即可得到所求范围;或将直线方程代入椭圆方程(圆方程)求得P,Q的纵坐标,由坐标之比,结合不等式的性质,即可得到所求范围.


科目:高中数学 来源: 题型:
【题目】为分析学生入学时的数学成绩对高一年级数学学习的影响,在高一年级学生中随机抽取10名学生,统计他们入学时的数学成绩和高一期末的数学成绩,如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩x(分) | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末 成绩y(分) | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)求相关系数r;
(2)求y关于x的线性回归方程;
(3)若某学生入学时的数学成绩为80分,试估计他高一期末的数学成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a、b、c(a<b<c).已知向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA)满足
=(cosC,cosA)满足 ![]()
![]() =
= ![]() (a+c).
(a+c).
(1)求证:a+c=2b;
(2)若2csinA﹣ ![]() a=0,且c﹣a=8,求△ABC的面积S.
a=0,且c﹣a=8,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥E-ABCD中,四边形ABCD是平行四边形,△BCE是等边三角形,△ABE是等腰直角三角形,∠BAE=90°,且AC=BC.

(1)证明:平面ABE⊥平面BCE;
(2)求二面角A-DE-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,x轴被曲线C2:y=x2-b截得的线段长度等于C1的短轴长.已知C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E.
,x轴被曲线C2:y=x2-b截得的线段长度等于C1的短轴长.已知C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E.
(1)求C1,C2的方程;
(2)求证:MA⊥MB;
(3)记△MAB,△MDE的面积分别为S1,S2,若![]() ,求λ的取值范围.
,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】8人围圆桌开会,其中正、副组长各1人,记录员1人.
(1)若正、副组长相邻而坐,有多少种坐法?
(2)若记录员坐于正、副组长之间,有多少种坐法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex﹣asinxcosx(a∈R,其中e是自然对数的底数).
(1)当a=0时,求f(x)的极值;
(2)若对于任意的x∈[0, ![]() ],f(x)≥0恒成立,求a的取值范围;
],f(x)≥0恒成立,求a的取值范围;
(3)是否存在实数a,使得函数f(x)在区间 ![]() 上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(点
两点(点![]() 均在第一象限),且直线
均在第一象限),且直线![]() 的斜率成等比数列,证明:直线
的斜率成等比数列,证明:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com