
【题目】已知函数![]() 的定义域是
的定义域是![]() ,对任意
,对任意![]() ,当
,当![]() 时,
时,![]() .关于函数
.关于函数![]() 给出下列四个命题:①函数
给出下列四个命题:①函数![]() 是周期函数;②函数
是周期函数;②函数![]() 是奇函数;③函数
是奇函数;③函数![]() 的全部零点为
的全部零点为![]() ;④当
;④当![]() 时,函数
时,函数![]() 的图象与函数
的图象与函数![]() 的图象有且只有三个公共点.其中真命题的序号为__________.
的图象有且只有三个公共点.其中真命题的序号为__________.
【答案】①③④
【解析】
①:利用![]() ,根据函数周期的定义可以判断出本命题的真假;
,根据函数周期的定义可以判断出本命题的真假;
②:利用奇函数的定义可以判断出本命题的真假;
③:结合函数的周期性和当![]() 时,
时,![]() ,可以判断出本命题的真假;
,可以判断出本命题的真假;
④:根据周期性画出当![]() 时,函数
时,函数![]() 的图象,在同一直角坐标系内画出函数
的图象,在同一直角坐标系内画出函数![]() 的图象,利用数形结合思想, 可以判断出本命题的真假;
的图象,利用数形结合思想, 可以判断出本命题的真假;
①:因为![]() ,所以
,所以![]() ,所以函数的周期是2,故本命题是真命题;
,所以函数的周期是2,故本命题是真命题;
②:因为![]() ,所以不符合奇函数的定义, 故本命题是假命题;
,所以不符合奇函数的定义, 故本命题是假命题;
③:当![]() 时,
时,![]() ,因此当
,因此当![]() 时,只有
时,只有![]() ,由①可知函数的周期是2,因此函数
,由①可知函数的周期是2,因此函数![]() 的全部零点为
的全部零点为![]() ,故本命题是真命题;
,故本命题是真命题;
④:当![]() 时,
时,![]() ,通过周期得到当
,通过周期得到当![]() 时,函数的图象,再画出函数
时,函数的图象,再画出函数![]() 的图象,如下图所示:
的图象,如下图所示:
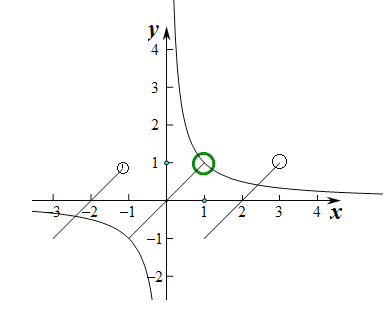
通过图象可知有三个不同的交点.故本命题是真命题.
故答案为:①③④


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数,![]() ),在以坐标原点为极点,
),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,等边
,等边![]() 的顶点都在
的顶点都在![]() 上,且点
上,且点![]() ,
,![]() ,
,![]() 依逆时针次序排列,点
依逆时针次序排列,点![]() 的极坐标为
的极坐标为![]() .
.
(1)求点![]() ,
,![]() ,
,![]() 的直角坐标;
的直角坐标;
(2)设![]() 为
为![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 距离的取值范围.
距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在复数范围内解方程![]() (
(![]() 为虚数单位)
为虚数单位)
(2)设![]() 是虚数,
是虚数,![]() 是实数,且
是实数,且![]()
(i)求![]() 的值及
的值及![]() 的实部的取值范围;
的实部的取值范围;
(ii)设![]() ,求证:
,求证:![]() 为纯虚数;
为纯虚数;
(iii)在(ii)的条件下求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①若直线![]() 平面
平面![]() ,直线
,直线![]() ,则
,则![]() ;②若直线l和平面
;②若直线l和平面![]() 内的无数条直线垂直,则直线l与平面
内的无数条直线垂直,则直线l与平面![]() 必相交;③过平面
必相交;③过平面![]() 外一点有且只有一条直线和平面
外一点有且只有一条直线和平面![]() 垂直;④过直线
垂直;④过直线![]() 外一点有且只有一个平面和直线a垂直
外一点有且只有一个平面和直线a垂直
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日.在平昌冬奥会短道速滑男子500米比赛中.中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.某高校为调查该校学生在冬奥会期间累计观看冬奥会的时间情况.收集了200位男生、100位女生累计观看冬奥会时间的样本数据(单位:小时).又在100位女生中随机抽取20个人.已知这20位女生的数据茎叶图如图所示.
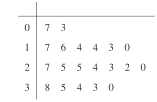
(1)将这20位女生的时间数据分成8组,分组区间分别为![]() ,在答题卡上完成频率分布直方图;
,在答题卡上完成频率分布直方图;
(2)以(1)中的频率作为概率,求1名女生观看冬奥会时间不少于30小时的概率;
(3)以(1)中的频率估计100位女生中累计观看时间小于20个小时的人数.已知200位男生中累计观看时间小于20小时的男生有50人请完成答题卡中的列联表,并判断是否有99 %的把握认为“该校学生观看冬奥会累计时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=-![]() x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.
(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视传媒为了解央视举办的“朗读者”节目的收视时间情况,随机抽取了某市名![]() 观众进行调查,其中有
观众进行调查,其中有![]() 名男观众和
名男观众和![]() 名女观众,将这
名女观众,将这![]() 名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在
名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在![]() 分钟以上(包括
分钟以上(包括![]() 分钟)的称为“朗读爱好者”,收视时间在
分钟)的称为“朗读爱好者”,收视时间在![]() 分钟以下(不包括
分钟以下(不包括![]() 分钟)的称为“非朗读爱好者”.
分钟)的称为“非朗读爱好者”.

(1)若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取![]() 名,再从这
名,再从这![]() 名观众中任选
名观众中任选![]() 名,求至少选到
名,求至少选到![]() 名“朗读爱好者”的概率;
名“朗读爱好者”的概率;
(2)若从收视时间在40分钟以上(包括40分钟)的所有观众中选出男、女观众各1名,求选出的这两名观众时间相差5分钟以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com