
 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围; <
< 都成立.
都成立.
 =
=  ,∵x=0时,f(x)取得极值,∴
,∵x=0时,f(x)取得极值,∴ =0,
=0, =0,解得a=1.经检验a=1符合题意. ……………4分
=0,解得a=1.经检验a=1符合题意. ……………4分 知
知
 ,由
,由 ,得
,得 ,令
,令 ,
, +b在[0,2]上恰有两个不同的实数根等价于φ(x)=0在[0,2]恰有两个不同实数根.
+b在[0,2]上恰有两个不同的实数根等价于φ(x)=0在[0,2]恰有两个不同实数根. ,
, ,于是
,于是 在(O,1)上单调递增;
在(O,1)上单调递增; ,于是
,于是 在(1,2)上单调递减.
在(1,2)上单调递减.
 .………………………………………8分
.………………………………………8分 的定义域为{x|x> -1},
的定义域为{x|x> -1}, , 令
, 令 =0得,x=0或x=
=0得,x=0或x=  (舍去),
(舍去), >0,f(x)单调递增; 当x>0时,
>0,f(x)单调递增; 当x>0时, <0,f(x)单调递减.
<0,f(x)单调递减. >0得,ln(
>0得,ln( +1)<
+1)<  +
+ ,
, )<
)< .……………………………………12分
.……………………………………12分

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
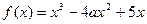 (
(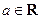 ).
).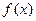 在区间[0, 2]上无极值, 求a的取值范围.
在区间[0, 2]上无极值, 求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com