
【题目】已知函数f(x)=ax﹣lnx﹣1.
(1)若函数f(x)在区间[1,+∞)上递增,求实数a的取值范围;
(2)求证:ln ![]() <
< ![]() (n∈N*).
(n∈N*).
科目:高中数学 来源: 题型:
【题目】已知圆 ![]() : x2+y2+Dx+Ey+3=0 ,圆
: x2+y2+Dx+Ey+3=0 ,圆 ![]() 关于直线 x+y-1=0对称,圆心在第二象限,半径为
关于直线 x+y-1=0对称,圆心在第二象限,半径为![]() .
.
(1)求圆 ![]() 的方程;
的方程;
(2)已知不过原点的直线 l 与圆 ![]() 相切,且在
相切,且在 ![]() 轴、
轴、 ![]() 轴上的截距相等,求直线 l 的方程.
轴上的截距相等,求直线 l 的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合M={x||x﹣ ![]() |
| ![]() },P={x|﹣1≤x≤4},则(UM)∩P等于( )
},P={x|﹣1≤x≤4},则(UM)∩P等于( )
A.{x|﹣4≤x≤﹣2}
B.{x|﹣1≤x≤3}
C.{x|3<x≤4}
D.{x|3≤x≤4}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=4sinθ,直线l的参数方程是 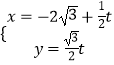 (t为参数).
(t为参数).
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x焦点为F,点D为其准线与x轴的交点,过点F的直线l与抛物线相交于A,B两点,则△DAB的面积S的取值范围为( )
A.[5,+∞)
B.[2,+∞)
C.[4,+∞)
D.[2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满分100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
[50,60) | 5 | 0.05 |
[60,70) | a | 0.20 |
[70,80) | 35 | b |
[80,90) | 25 | 0.25 |
[90,100) | 15 | 0.15 |
合计 | 100 | 1.00 |
(I)求a,b的值及随机抽取一考生恰为优秀生的概率;
(Ⅱ)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;
(Ⅲ)在第(Ⅱ)问抽取的优秀生中指派2名学生担任负责人,求至少一人的成绩在[90,100]的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com