
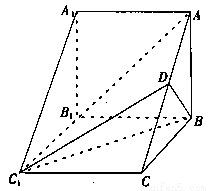
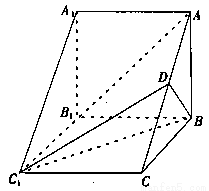
如图,在三棱柱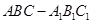 中,侧棱
中,侧棱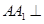 底面
底面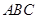 ,
,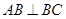 ,
,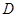 为
为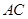 的中点,
的中点,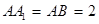 .
.
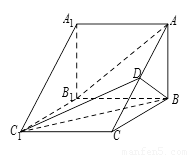
(Ⅰ)求证: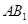 //平面
//平面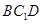 ;
;
(Ⅱ)设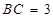 ,求四棱锥
,求四棱锥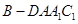 的体积.
的体积.
(Ⅰ)详见解析;(Ⅱ)体积为3.
【解析】
试题分析:(Ⅰ)为了证明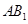 //平面
//平面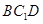 ,需要在平面
,需要在平面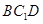 内找一条与
内找一条与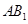 平行的直线,而要找这条直线一般通过作过
平行的直线,而要找这条直线一般通过作过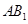 且与平面
且与平面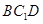 相交的平面来找.在本题中联系到
相交的平面来找.在本题中联系到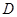 为
为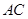 中点,故连结
中点,故连结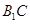 ,这样便得一平面
,这样便得一平面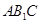 ,接下来只需证
,接下来只需证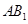 与平面
与平面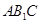 和平面
和平面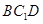 的交线平行即可.
的交线平行即可.

(Ⅱ)底面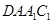 为一直角梯形,故易得其面积,本题的关键是求出点B到平面
为一直角梯形,故易得其面积,本题的关键是求出点B到平面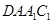 的距离.由于
的距离.由于 平面
平面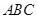 ,所以易得平面
,所以易得平面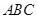
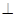 平面
平面 .平面
.平面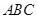
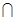 平面
平面
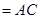 .根据两平面垂直的性质定理知,只需过B作交线AC的垂线即可得点B到平面
.根据两平面垂直的性质定理知,只需过B作交线AC的垂线即可得点B到平面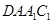 的距离,从而求出体积.
的距离,从而求出体积.
试题解析:(Ⅰ)连接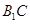 ,设
,设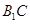 与
与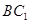 相交于点
相交于点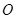 ,连接
,连接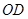 ,
,

∵ 四边形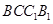 是平行四边形,
是平行四边形,
∴点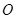 为
为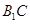 的中点.
的中点.
∵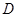 为
为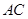 的中点,∴
的中点,∴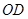 为△
为△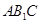 的中位线,
的中位线,
∴ 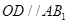 .
.
∵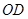
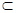 平面
平面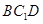 ,
,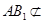 平面
平面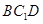 ,
,
∴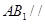 平面
平面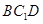 .
6分
.
6分
(Ⅱ) ∵ 平面
平面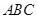 ,
,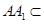 平面
平面 ,
,
∴ 平面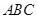
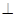 平面
平面 ,且平面
,且平面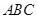
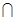 平面
平面
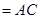 .
.
作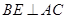 ,垂足为
,垂足为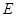 ,则
,则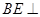 平面
平面 ,
,
∵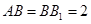 ,
,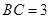 ,
,
在Rt△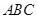 中,
中,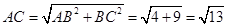 ,
,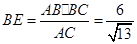 ,
,
∴四棱锥 的体积
的体积

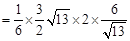
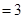 12分
12分
考点:1、直线与平面的位置关系;2、多面体的体积.


科目:高中数学 来源:2014届广东省高三上学期开学摸底联考文科数学试卷(解析版) 题型:解答题
如图,在三棱柱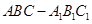 中,侧棱
中,侧棱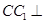 底面
底面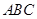 ,
,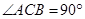 ,
,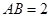 ,
,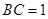 ,
,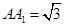 .
.

(1)证明: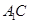
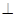 平面
平面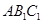 ;
;
(2)若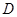 是棱
是棱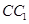 的中点,在棱
的中点,在棱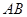 上是否存在一点
上是否存在一点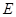 ,使
,使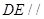 平面
平面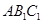 ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高一下学期期末考试理科数学试卷(解析版) 题型:填空题
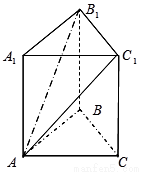
如图,在三棱柱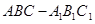 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则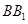 与平面
与平面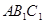 所成的角的大小为
所成的角的大小为
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一6月月考数学试卷(解析版) 题型:解答题
如图,在三棱柱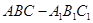 中,侧棱
中,侧棱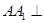 底面
底面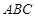 ,
,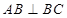 ,
,
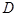 为
为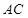 的中点,
的中点,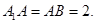
(1)求证: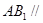 平面
平面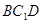 ;
;
(2)过点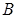 作
作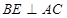 于点
于点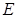 ,求证:直线
,求证:直线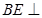 平面
平面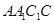
(3)若四棱锥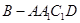 的体积为3,求
的体积为3,求 的长度
的长度
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下学期期中考试数学试卷(解析版) 题型:解答题
如图,在三棱柱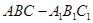 中,侧棱
中,侧棱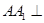 底面
底面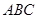 ,
,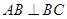 ,
,
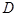 为
为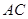 的中点,
的中点,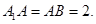
(1)求证: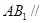 平面
平面 ;
;
(2)过点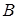 作
作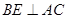 于点
于点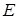 ,求证:直线
,求证:直线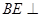 平面
平面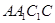
(3)若四棱锥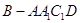 的体积为3,求
的体积为3,求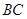 的长度
的长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com