
【题目】已知函数 ![]() 的部分图象如图所示.
的部分图象如图所示.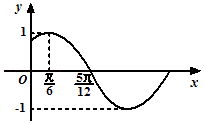
(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,若(2a﹣c)cosB=bcosC,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)
解:由图象知A=1, ![]() ,∴ω=2,
,∴ω=2,
∴f(x)=sin(2x+φ)
∵图象过( ![]() ),将点(
),将点( ![]() )代入解析式得
)代入解析式得 ![]() ,
,
∵ ![]() ,
,
∴ ![]()
故得函数 ![]()
(2)
解:由(2a﹣c)cosB=bcosC,
根据正弦定理,得:(2sinA﹣sinC)cosB=sinBcosC
∴2sinAcosB=sin(B+C),
∴2sinAcosB=sinA.
∵A∈(0,π),
∴sinA≠0,
∴cosB= ![]() ,即B=
,即B= ![]()
∴A+C= ![]() ,即
,即 ![]()
那么: ![]() ,
,
![]()
故得 ![]()
【解析】(1)根据图象求出A,ω 和φ,即可求函数f(x)的解析式;(2)利用正弦定理化简,求出B,根据三角内角定理可得A的范围,利用函数解析式之间的关系即可得到结论


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+ ![]() x2在x=﹣1处取得极大值,记g(x)=
x2在x=﹣1处取得极大值,记g(x)= ![]() .程序框图如图所示,若输出的结果S>
.程序框图如图所示,若输出的结果S> ![]() ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( ) 
A.n≤2014?
B.n≤2015?
C.n>2014?
D.n>2015?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴的正半轴上,过点F的直线l与抛物线C相交于A、B两点,且满足 ![]() .
.
(1)求抛物线C的标准方程;
(2)若点M在抛物线C的准线上运动,其纵坐标的取值范围是[﹣1,1],且 ![]() ,点N是以线段AB为直径的圆与抛物线C的准线的一个公共点,求点N的纵坐标的取值范围.
,点N是以线段AB为直径的圆与抛物线C的准线的一个公共点,求点N的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB= ![]() PD.
PD.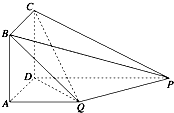
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q﹣BP﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2≠0”
B.“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件
C.若命题P:n∈N,2n>1000,则﹣P:n∈N,2n≤1000
D.命题“x∈(﹣∞,0),2x<3x”是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+b)lnx,g(x)=alnx+ ![]() ﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
﹣x(a≠1),已知曲线y=f(x)在点(1,f(1))处的切线与直线x+2y=0垂直.
(1)求b的值;
(2)若对任意x≥1,都有g(x)> ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c
(1)若a,b,c成等比数列, ![]() ,求
,求 ![]() 的值;
的值;
(2)若A,B,C成等差数列,且b=2,设A=α,△ABC的周长为l,求l=f(α)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有1 000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数见右上表,据此估计这1 000根中纤维长度不小于37.5 mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ⊥
⊥ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |=t,若P点是△ABC所在平面内一点,且
|=t,若P点是△ABC所在平面内一点,且 ![]() =
= ![]() +
+ ![]() ,当t变化时,
,当t变化时, ![]() 的最大值等于( )
的最大值等于( )
A.﹣2
B.0
C.2
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com