
【题目】直线y=ax+1与双曲线3x2﹣y2=1相交于A、B两点.
(1)求AB的长;
(2)当a为何值时,以AB为直径的圆经过坐标原点?
【答案】
(1)解:由 ![]() ∴
∴ ![]()
∵相交于A、B两点,设A(x1,y1),B(x2,y2)
∴△=(2a)2﹣4(a2﹣3)2>0,
∴ ![]() 且
且 ![]()
∴ ![]() ,(*)
,(*)
∴ ![]() (
( ![]() 且
且 ![]() )
)
(2)解:由(1)中(*)式得: ![]() ,
,
∵以AB为直径的圆经过坐标原点
∴ ![]() =0,∴x1x2+y1y2=0
=0,∴x1x2+y1y2=0
∴x1x2+(ax1+1)(ax2+1)=0 即(1+a2)x1x2+a(x1+x2)+1=0
∴ ![]()
∴a=±1.
【解析】(1)将直线与双曲线相交于两点转化为一元二次方程有两个根,从而求得a的取值范围,并利用求根公式将两点的横坐标用a表示出来,进而求得线段AB的长;(2)将几何问题转化为向量问题,向量问题再转化为代数式问题,进而根据根与系数的关系求得实数a的值.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,椭圆C1: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2:
=1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为e1;双曲线C2: ![]() ﹣
﹣ ![]() =1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2=
=1的左、右焦点分别为F3 , F4 , 离心率为e2 , 已知e1e2= ![]() ,且|F2F4|=
,且|F2F4|= ![]() ﹣1.
﹣1.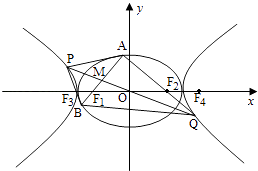
(Ⅰ)求C1、C2的方程;
(Ⅱ)过F1作C1的不垂直于y轴的弦AB,M为AB的中点,当直线OM与C2交于P,Q两点时,求四边形APBQ面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|(x﹣3)(x﹣3a﹣5)<0},函数y=lg(﹣x2+5x+14)的定义域为集合B.
(1)若a=4,求集合A∩B;
(2)若“x∈A”是“x∈B”的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() .
.
(1)求圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() ,求直线
,求直线![]() 被圆
被圆![]() 所截得弦长的最大值;
所截得弦长的最大值;
(3)若直线![]() 是圆心
是圆心![]() 下方的切线,当
下方的切线,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有同一型号的电脑96台,为了了解这种电脑每开机一次所产生的辐射情况,从中抽取10台在同一条件下做开机实验,测量开机一次所产生的辐射,得到如下数据:
13.7 12.9 14.4 13.8 13.3
12.7 13.5 13.6 13.1 13.4
(1)写出采用简单随机抽样抽取上述样本的过程;
(2)根据样本,请估计总体平均数与总体标准差的情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列4个命题: ①“若a、G、b成等比数列,则G2=ab”的逆命题;
②“如果x2+x﹣6≥0,则x>2”的否命题;
③在△ABC中,“若A>B”则“sinA>sinB”的逆否命题;
④当0≤α≤π时,若8x2﹣(8sinα)x+cos2α≥0对x∈R恒成立,则α的取值范围是0≤α≤ ![]() .
.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为  (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12.
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为3ρ2cos2θ+4ρ2sin2θ=12.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)已知直线l与曲线C交于A,B两点,试求|AB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com