
【题目】已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y)且当x>0,f(x)<0.
给出下列四个结论:
①f(0)=0;②f(x)为偶函数;
③f(x)为R上减函数;④f(x)为R上增函数.
其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据题意,令y=x=0计算f(0)的值,判断①正确;
令y=-x,得出f(-x)=-f(x),f(x)是奇函数,判断②错误;
根据x>0,f(x)<0,x=0时f(x)=0,x<0时,f(x)>0,
判断f(x)为R上的减函数,③正确,④错误.
解:对于①,令x=y=0,则f(0)=f(0)+f(0)=2f(0),∴f(0)=0,①正确;
对于②,令y=-x,则f(x-x)=f(x)+f(-x)=0,∴f(-x)=-f(x),f(x)是奇函数,②错误;
对于③,)f(x)是R上的减函数,证明如下:
任取x1,x2∈R,x1<x2,则x2﹣x1>0
∴f(x2)﹣f(x1)=f(x2﹣x1+x1)﹣f(x1)=f(x2﹣x1)+f(x1)﹣f(x1)=f(x2﹣x1)<0
∴f(x1)>f(x2)
故f(x)是R上的减函数.③正确,④错误.
综上,其中正确的结论是①③.
故选:A.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】如图,点P(0,﹣1)是椭圆C1: ![]() +
+ ![]() =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1 , l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D. 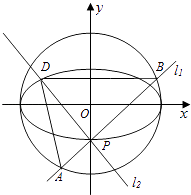
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4; 白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率.
(2)在取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下结论正确的序号有_________
(1)根据![]() 列联表中的数据计算得出
列联表中的数据计算得出![]() ≥6.635, 而P(
≥6.635, 而P(![]() ≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系.
≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系.
(2)在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关.
(3)在线性回归分析中,相关系数为![]() ,
,![]() 越接近于1,相关程度越大;
越接近于1,相关程度越大;![]() 越小,相关程度越小.
越小,相关程度越小.
(4)在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15.
的值一定是15.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时候相差不超过2秒的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P1 , P2 , …Pn为平面α内的n个点,在平面α内的所有点中,若点P到点P1 , P2 , …Pn的距离之和最小,则称点P为P1 , P2 , …Pn的一个“中位点”,例如,线段AB上的任意点都是端点A,B的中位点,现有下列命题:
①若三个点A、B、C共线,C在线段AB上,则C是A,B,C的中位点;
②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点A、B、C、D共线,则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“圆材埋壁”是《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,学会一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知道大小,用锯取锯它,锯口深一寸,锯道长一尺,问这块圆柱形木材的直径是多少?现有圆柱形木材一部分埋在墙壁中,截面如图所示,已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,则阴影部分面积约为(注:
寸,则阴影部分面积约为(注:![]() ,
,![]() ,1尺=10寸)( )
,1尺=10寸)( )

A. 6.33平方寸B. 6.35平方寸
C. 6.37平方寸D. 6.39平方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com