
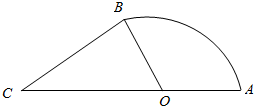
 广告公司为某游乐场设计某项设施的宣传画,根据该设施的外观,设计成的平面图由半径为2m的扇形AOB和三角区域BCO构成,其中C,O,A在一条直线上,∠ACB=$\frac{π}{4}$,记该设施平面图的面积为S(x)m2,∠AOB=xrad,其中$\frac{π}{2}$<x<π.
广告公司为某游乐场设计某项设施的宣传画,根据该设施的外观,设计成的平面图由半径为2m的扇形AOB和三角区域BCO构成,其中C,O,A在一条直线上,∠ACB=$\frac{π}{4}$,记该设施平面图的面积为S(x)m2,∠AOB=xrad,其中$\frac{π}{2}$<x<π.分析 (1)首先,求解三角形和扇形的面积,然后,求和即可得到相应的解析式;
(2)根据三角函数辅助角公式和导数的计算等知识求解其最大值即可.
解答 解:(1)∵扇形AOB的半径为2m,∠AOB=xrad,
∴S扇形=$\frac{1}{2}$x•22=2x,
过点B作边AC的垂线,垂足为D,如图所示: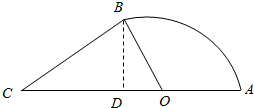
则∠BOD=π-x,
∴BD=2sin(π-x)=2sinx,OD=2cos(π-x)=-2cosx,
∵∠ACB=$\frac{π}{4}$,
∴CD=BD=2sinx,
∴S△BOC=$\frac{1}{2}$CO•BD=$\frac{1}{2}$(2sinx-2cosx)×2sinx=2sin2x-2sinxcosx=1-cos2x-sin2x,
∴S(x)=1-cos2x-sin2x+2x,
(2)根据(1),得到S(x)=1-cos2x-sin2x+2x,
∴S′(x)=2sin2x-2cos2x+2,
令S′(x)=0,
∴2$\sqrt{2}$sin(2x-$\frac{π}{4}$)=-2,
∴sin(2x-$\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$,
∴2x-$\frac{π}{4}$=$\frac{5π}{4}$,
∴x=$\frac{3π}{4}$,
根据实际意义知,当x=$\frac{3π}{4}$时,该函数取得最大值,
故设计∠AOB=$\frac{3π}{4}$时,此时S(x)有最大值.
点评 本题重点考查了三角形的面积公式、辅助角公式、三角函数的图象与性质等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
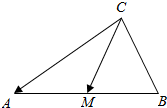
| A. | $\overrightarrow a-2\overrightarrow b$ | B. | $\overrightarrow a+2\overrightarrow b$ | C. | $2\overrightarrow a-\overrightarrow b$ | D. | $2\overrightarrow a+\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com