
【题目】如图,在正三棱柱![]() 中,
中,![]() ,D,E,F分别为线段
,D,E,F分别为线段![]() ,
,![]() ,
,![]() 的中点.
的中点.
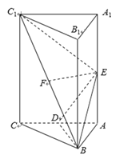
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)过![]() 作截面与线段
作截面与线段![]() 交于点H,使得
交于点H,使得![]() 平面
平面![]() ,试确定点H的位置,并给出证明;
,试确定点H的位置,并给出证明;
(2)在(1)的条件下,若二面角![]() 的大小为
的大小为![]() ,试求直线
,试求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x+b|,ab>0.
(1)当a=1,b=1时,求不等式f(x)<3的解集;
(2)若f(x)的最小值为2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
岁之间的200人进行调查,并按年龄绘制出频率分布直方图,如图.
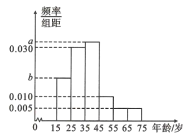
若把年龄在区间![]() ,
,![]() 内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为
内的人分别称为“青少年”“中老年”.经统计“青少年”和“中老年”的人数之比为![]() .其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为
.其中“青少年”中有40人关注“两会”,“中老年”中关注“两会”和不关注“两会”的人数之比为![]() .
.
(1)求图中![]() 的值.
的值.
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
中随机抽取8人作为代表,从8人中任选2人,求2人都是“中老年”的概率.
(3)根据已知条件,完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() %的把握认为“中老年”比“青少年”更加关注“两会”.
%的把握认为“中老年”比“青少年”更加关注“两会”.
关注 | 不关注 | 总计 | |
“青少年” | |||
“中老年” | |||
总计 |
附: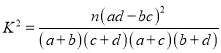 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
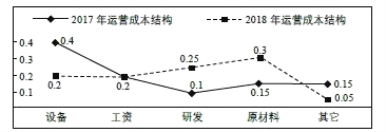
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]()
(Ⅰ)求数列![]() 的通项
的通项![]() ,及前
,及前![]() 项和
项和![]()
(Ⅱ)请你在数列![]() 的前4项中选出三项,组成公比的绝对值小于1的等比数列
的前4项中选出三项,组成公比的绝对值小于1的等比数列![]() 的前3项,并记数列
的前3项,并记数列![]() 的前n项和为
的前n项和为![]() .若对任意正整数
.若对任意正整数![]() ,不等式
,不等式![]() 恒成立,试求
恒成立,试求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com