
【题目】设函数f(x)=x2ex﹣1﹣ ![]() x3﹣x2(x∈R).
x3﹣x2(x∈R).
(1)求函数f(x)的单调区间;
(2)当x∈(1,+∞)时,用数学归纳法证明:n∈N* , ex﹣1> ![]() (其中n!=1×2×…×n).
(其中n!=1×2×…×n).
【答案】
(1)解:f′(x)=2xex﹣1+x2ex﹣1﹣x2﹣2x=x(x+2)(ex﹣1﹣1),
令f′(x)=0,可得x1=﹣2,x2=0,x3=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x | (﹣∞,﹣2) | ﹣2 | (﹣2,0) | 0 | (0,1) | 1 | (1,+∞) |
f'(x) | ﹣ | 0 | + | 0 | ﹣ | 0 | + |
f(x) | ↓ | 极小值 | ↑ | 极大值 | ↓ | 极小值 | ↑ |
所以函数y=f(x)的增区间为(﹣2,0)和(1,+∞),减区间为(﹣∞,﹣2)和(0,1)
(2)证明:设gn(x)=ex﹣1﹣ ![]() ,
,
当n=1时,只需证明g1(x)=ex﹣1﹣x>0,当x∈(1,+∞)时,g1′(x)=ex﹣1﹣1>0,
所以g1(x)=ex﹣1﹣x在(1,+∞)上是增函数,
所以g1(x)>g1(1)=e0﹣1=0,即ex﹣1>x;
当x∈(1,+∞)时,假设n=k时不等式成立,即gk(x)=ex﹣1﹣ ![]() >0,
>0,
当n=k+1时,
因为g′k+1(x)=ex﹣1﹣ ![]() =ex﹣1﹣
=ex﹣1﹣ ![]() >0,
>0,
所以gk+1(x)在(1,+∞)上也是增函数.
所以gk+1(x)>gk+1(1)=e0﹣ ![]() >0,
>0,
即当n=k+1时,不等式成立.
由归纳原理,知当x∈(1,+∞)时,n∈N*,ex﹣1> ![]()
【解析】(1)利用导数求函数的单调区间,关键点有二,一是求对导函数,二是解不等式f′(x)>0,得到x的范围,再兼顾函数的定义域,列出当x变化时,f′(x),f(x)的变化情况表,将能很轻松的解答问题;(2)本问根据要证明的不等式:n∈N* , ex﹣1> ![]() .构造出函数设gn(x)=ex﹣1﹣
.构造出函数设gn(x)=ex﹣1﹣ ![]() ,在利用数学归纳法证明出当n∈N*时有假设n=k时不等式成立,即gk(x)=ex﹣1﹣
,在利用数学归纳法证明出当n∈N*时有假设n=k时不等式成立,即gk(x)=ex﹣1﹣ ![]() >0,这还要借助于导数来解答.
>0,这还要借助于导数来解答.
【考点精析】利用利用导数研究函数的单调性和数学归纳法的定义对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间内,(1)如果
![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;数学归纳法是证明关于正整数n的命题的一种方法.
在这个区间单调递减;数学归纳法是证明关于正整数n的命题的一种方法.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积为S= ![]() bccosA.
bccosA.
(1)求角A的大小;
(2)若c=8,点D在AC边上,且CD=2,cos∠ADB=﹣ ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函致y=f(x),恒有f(x+4)=f(x)﹣f(﹣2)成立,且f(0)=1,当0≤x1<x2≤2时, ![]() <0,则方程f(x)﹣lg|x|=0的根的个数为( )
<0,则方程f(x)﹣lg|x|=0的根的个数为( )
A.12
B.10
C.6
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数λ>0,设函数f(x)=eλx﹣x.
(Ⅰ)当λ=1时,求函数f(x)的极值;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≥0恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足an+Sn=2.
(1)求数列{an}的通项公式;
(2)求证数列{an}中不存在三项按原来顺序成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示的几何体中, ![]() 为三棱柱,且
为三棱柱,且![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() .
.
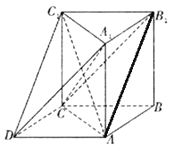
(1)求证: ![]() ;
;
(2)若![]() ,求证:
,求证: ![]() ;
;
(3)若![]() ,二面角
,二面角![]() 的余弦值为若
的余弦值为若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,设直线
,设直线![]() 的斜率是
的斜率是![]() ,且
,且![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的标准方程.
(Ⅱ)若直线![]() 在
在![]() 轴上的截距是
轴上的截距是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)以![]() 为底作等腰三角形,顶点为
为底作等腰三角形,顶点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
(1)当![]() 时,
时, ![]() ,若当
,若当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)若![]() 的图像关于
的图像关于![]() 对称,且
对称,且![]() 时,
时, ![]() ,求当
,求当![]() 时,
时, ![]() 的解析式;
的解析式;
(3)当![]() 时,
时, ![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆 ![]() 的左、右焦点,F2在以
的左、右焦点,F2在以 ![]() 为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.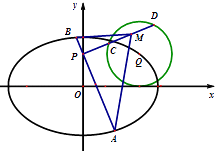
(1)求椭圆C1的方程;
(2)过点P(0,1)的直线l1交椭圆C1于A,B两点,过P与l1垂直的直线l2交圆C2于C,D两点,M为线段CD中点,求△MAB面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com