
【题目】已知函数![]() ,(其中
,(其中![]() ),
),![]() .
.
(1)若![]() 对定义域内的任意实数x恒成立,求实数a的取值范围;
对定义域内的任意实数x恒成立,求实数a的取值范围;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 与
与![]() 轴交于
轴交于![]() 两点.以坐标原点
两点.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 在第一象限交于点
在第一象限交于点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电信运营公司为响应国家5G网络建设政策,拟实行5G网络流量阶梯定价.每人月用流量中不超过![]() (一种流量计算单位)的部分按2元
(一种流量计算单位)的部分按2元![]() 收费;超出
收费;超出![]() 的部分按4元
的部分按4元![]() 收费.从用户群中随机调查了10000位用户,获得了他们某月的流量使用数据.整理得到如下的频率分布直方图:
收费.从用户群中随机调查了10000位用户,获得了他们某月的流量使用数据.整理得到如下的频率分布直方图:

(1)若![]() 为整数,依据本次调查,为使80
为整数,依据本次调查,为使80![]() 以上用户在该月的流量价格为2元
以上用户在该月的流量价格为2元![]() ,
,![]() 至少定为多少?
至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当![]() 时,试估计用户该月的人均流量费.
时,试估计用户该月的人均流量费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由n(n∈N*)个正整数构成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),记SA=a1+a2+…+an,对于任意不大于SA的正整数m,均存在集合A的一个子集,使得该子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求证:“a1,a2,…,an成等差数列”的充要条件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值时an的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福、敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福、敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
| 是 | 否 | 合计 |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式:![]()
![]()
![]() .
.
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
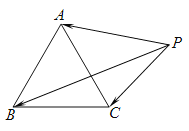
【题目】如图,![]() 是边长为1的正三角形,点P在
是边长为1的正三角形,点P在![]() 所在的平面内,且
所在的平面内,且![]() (a为常数),下列结论中正确的是( )
(a为常数),下列结论中正确的是( )
A.当![]() 时,满足条件的点P有且只有一个
时,满足条件的点P有且只有一个
B.当![]() 时,满足条件的点P有三个
时,满足条件的点P有三个
C.当![]() 时,满足条件的点P有无数个
时,满足条件的点P有无数个
D.当a为任意正实数时,满足条件的点总是有限个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,分别过
两点,分别过![]() ,
,![]() 作抛物线
作抛物线![]() 的切线,两切线交于点
的切线,两切线交于点![]() .
.
(1)若直线![]() 变动时,点
变动时,点![]() 始终在以
始终在以![]() 为直径的圆上,求动点
为直径的圆上,求动点![]() 的轨迹方程;
的轨迹方程;
(2)设圆![]() ,若直线
,若直线![]() 与圆
与圆![]() 相切于点
相切于点![]() (点
(点![]() 在线段
在线段![]() 上).是否存在点
上).是否存在点![]() 使得
使得![]() ?若存在,求出点
?若存在,求出点![]() 坐标,若不存在,说明理由.
坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com