
【题目】已知椭圆C: ![]() =1(a>b>0)与直线x+y﹣1=0相交于A、B两点,若a∈[
=1(a>b>0)与直线x+y﹣1=0相交于A、B两点,若a∈[ ![]() ,
, ![]() ],且以AB为直径的圆经过坐标原点O,则椭圆离心率e的取值范围为 .
],且以AB为直径的圆经过坐标原点O,则椭圆离心率e的取值范围为 .
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1= ![]() ,a2=
,a2= ![]() ,2an=an+1+an﹣1(n≥2,n∈N),数列{bn}满足:b1<0,3bn﹣bn﹣1=n(n≥2,n∈R),数列{bn}的前n项和为Sn .
,2an=an+1+an﹣1(n≥2,n∈N),数列{bn}满足:b1<0,3bn﹣bn﹣1=n(n≥2,n∈R),数列{bn}的前n项和为Sn .
(1)求证:数列{bn﹣an}为等比数列;
(2)求证:数列{bn}为递增数列;
(3)若当且仅当n=3时,Sn取得最小值,求b1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),将f(x)图像沿x轴向右平移 ![]() 个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣
个单位,然后把所得到图像上每一点的纵坐标保持不变,横坐标扩大到原来的2倍,这样得到的曲线与y=2sin(x﹣ ![]() )的图像相同,那么y=f(x)的解析式为( )
)的图像相同,那么y=f(x)的解析式为( )
A.f(x)=2sin(2x﹣ ![]() )
)
B.f(x)=2sin(2x﹣ ![]() )
)
C.f(x)=2sin(2x+ ![]() )
)
D.f(x)=2sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线l⊥平面α,垂足为O,已知△ABC中,∠ABC为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1)A∈l,(2)B∈α.则C、O两点间的最大距离为 . 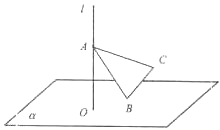
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)如图,已知四棱锥P–ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.

(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用p(万元)和宿舍与工厂的距离x(km)的关系为:p= ![]() (0≤x≤8),若距离为1km时,宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
(0≤x≤8),若距离为1km时,宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
(1)求f(x)的表达式,并写出其定义域;
(2)宿舍应建在离工厂多远处,可使总费用f(x)最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂要建造一个长方体无盖贮水池,其容积为6400m3 , 深为4m,如果池底每1m2的造价为300元,池壁每1m2的造价为240元,问怎样设计水池能使总造价最低,最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.
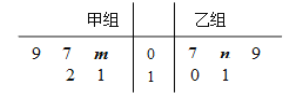
(1)分别求出![]() 的值;
的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差![]() 和
和![]() ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人加工的合格零件个数之和大于17,则称该车间“质量合格”,求该车间“质量合格”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com