
����Ŀ�����Ķ����в��ϣ���������ʵ��a1 �� a2����a12+a22=1����ôa1+a2 ![]() ��֤�������캯��f��x��=��x��a1��2+��x��a2��2=2x2��2��a1+a2��x+1����Ϊ��һ��ʵ��x������f��x����0�����ԡ���0���Ӷ���4��a1+a2��2��8��0������a1+a2
��֤�������캯��f��x��=��x��a1��2+��x��a2��2=2x2��2��a1+a2��x+1����Ϊ��һ��ʵ��x������f��x����0�����ԡ���0���Ӷ���4��a1+a2��2��8��0������a1+a2 ![]() ����������֤����������n����ʵ������a12+a22+��+an2=1ʱ�����ܵõ��Ľ���Ϊ ��
����������֤����������n����ʵ������a12+a22+��+an2=1ʱ�����ܵõ��Ľ���Ϊ ��
���𰸡�a1+a2+��+an�� ![]()
���������⣺���캯��f��x��=��x��a1��2+��x��a2��2+��+��x��an��2=nx2��2��a1+a2+��+an��x+1��
�ɶ�һ��ʵ��x������f��x����0�����ԡ���0����a1+a2+��+an�� ![]()
���Դ��ǣ�a1+a2+��+an�� ![]()
�����㾫�����������⣬������Ҫ�˽��������(�������ͬ����֮�����ijЩ����(��һ��)��,�Ʋ�����һ���������������һ���������Ƶ����ʵ�����,�����������)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}����a1=1�� ![]() ����ǰn���ΪSn �� ��
����ǰn���ΪSn �� ��
��1��a5=��
��2��S2n= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��2mx+10��m��1����
��1����f��m��=1������f��x���Ľ���ʽ��
��2����f��x�������䣨���ޣ�2]���Ǽ��������Ҷ��������x1 �� x2��[1��m+1]��|f��x1����f��x2��|��9���������ʵ��m��ȡֵ��Χ��
��3����f��x��������[3��5]������㣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��麯����ͬһ�������ǣ� ��
�� ![]() ��
�� ![]() ��
��
��f��x��=x�� ![]() ��
��
��f��x��=x0�� ![]() ��
��
��f��x��=x2��2x��1��g��t��=t2��2t��1��
A.�٢�
B.�٢�
C.�ۢ�
D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����g��x��=aln x��f��x��=x3+x2+bx��
��1����f��x��������[1��2]�ϲ��ǵ�����������ʵ��b�ķ�Χ��
��2����������x��[1��e]������g��x���ݩ�x2+��a+2��x���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������߹���x��Գƣ����Ķ���������ԭ�㣬��P��1��2����A��x1 �� y1����B��x2 �� y2�������������ϣ� 
��1��д���������ߵķ��̼����߷��̣�
��2����PA��PB��б�ʴ�������б�ǻ���ʱ����y1+y2��ֵ��ֱ��AB��б�ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lg��ax2+ax+2����a��R����
��1����a=��1����f��x���ĵ������䣻
��2��������f��x���Ķ�����ΪR����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=ax��a��0��a��1���뺯��y=��a��1��x2��2x��1��ͬһ����ϵ�ڵ�ͼ������ǣ� ��
A.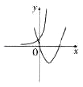
B.
C.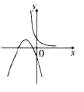
D.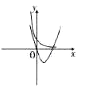
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x��=ax2+bx��3��x=1��ȡ�ü�ֵ�����ڣ�0����3���㴦��������ֱ��2x+y=0ƽ�У� ������f��x���Ľ���ʽ��
��������g��x��=xf��x��+4x�ĵ����������䣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com