练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知

    （1）最小正周期及对称轴方程；

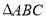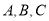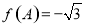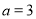    （2）已知锐角的内角的对边分别为，且 ,，求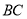边上的高的最大值．

     

    （1） （2）

    【解析】

    试题分析：（1）f（x）解析式利用二倍角的正弦、诱导公式化简，整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数，代入周期公式即可求出f（x）的最小正周期，根据正弦函数的对称性即可确定出对称轴方程；

    （2）由，根据第一问确定出的f（x）解析式，求出A的度数，利用余弦定理列出关系式，利用基本不等式求出bc的最小值，将sinA，bc的最小值代入三角形面积公式求出△ABC的面积，然后在求出h的最大值即可．

    （1）

    （2）由得

    由余弦定理得

    设边上的高为，由三角形等面积法知

    ，即的最大值为

    考点：1．余弦定理；2．正弦函数的对称性和周期；2．基本不等式的运用．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年河北省高三年级模拟考试文科数学试卷（解析版） 题型：选择题

    若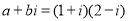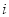（是虚数单位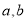，是实数），则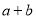的值是（ ）

    （A）2 （B）3 （C）4 （D）5

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷（解析版） 题型：选择题

    若平面内两个向量与共线，则等于 （ ）

    A．　　　　　 B．　　　　　 C．　　　　 　 D．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省盟校高三第二次联考理科数学试卷（解析版） 题型：选择题

    单位向量，且，则的最小值为（ ）

    A． B．1 C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省盟校高三第二次联考文科数学试卷（解析版） 题型：解答题

    已知函数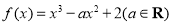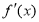，为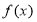的导函数。 （1）求函数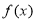的单调递减区间；

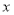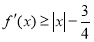    （2）若对一切的实数，有成立，求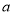的取值范围；

    （3）当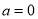时，在曲线上是否存在两点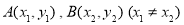，使得曲线在 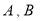两点处的切线均与直线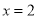交于同一点？若存在，求出交点纵坐标的最大值；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省盟校高三第二次联考文科数学试卷（解析版） 题型：填空题

    已知向量，且∥，则________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省盟校高三第二次联考文科数学试卷（解析版） 题型：选择题

    对于实数和，定义运算，运算原理如右图所示，则式子的值为（ ）

    A．6 B．7 C．8 D．9

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省盟校高三第一次联考理科数学试卷（解析版） 题型：选择题

    给出下列命题，其中真命题的个数是( )

    ①存在，使得成立;

    ②对于任意的三个平面向量、、，总有成立;

    ③相关系数 ()，值越大，变量之间的线性相关程度越高.

    A．0 B．1 C．2 D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西省宜春市高三考前模拟理科数学试卷（解析版） 题型：填空题

    执行下图所示的程序框图，若输入A=2014，B=125，输出的A的值是____ ．

     

     

    查看答案和解析>>

    同步练习册答案