
����Ŀ���й��Ŵ����Ҫ��ѧ���������ֻ������գ����֡��䡢�����顢������ơ����ա���ij��ѧΪ������ա��Ĵ�ͳ�Ļ����ֱ����������Ϊ�����֡��䡢�����顢����������ͳ�Ļ�֪ʶ�ľ��������мס��ҡ�����λѡ�ֽ�����ǰ�����������𡢹涨��ÿ��֪ʶ����ǰ�����ĵ÷ֶ��ֱ�Ϊ![]() ��
��![]() ����
����![]() ����ѡ�����÷�Ϊ�����÷�֮�ͣ���������������֪�����÷�Ϊ26�֣��Һͱ����÷ֶ�Ϊ11�֣�����������һ�������л�õ�һ����������������ȷ���ǣ� ��
����ѡ�����÷�Ϊ�����÷�֮�ͣ���������������֪�����÷�Ϊ26�֣��Һͱ����÷ֶ�Ϊ11�֣�����������һ�������л�õ�һ����������������ȷ���ǣ� ��
A. ÿ��������һ���÷�![]() Ϊ4 B. ������һ��������õڶ���
Ϊ4 B. ������һ��������õڶ���
C. �����ij�������õ����� D. ��������һ��������õ�һ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() Ϊ������������У�
Ϊ������������У� ![]() ��
��![]() ��Ϊ�ȱ������Σ���ƽ��
��Ϊ�ȱ������Σ���ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() .
.

��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2���������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ����
����
������![]() ������
������![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����������![]() ���������켫ֵ��
���������켫ֵ��![]() ��
�� ![]() ����֤��
����֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=aln��2x+1��+bx+1��
��1��������y=f��x����x=1��ȡ�ü�ֵ��������y=f��x���ڵ㣨0��f��0��������������ֱ��2x+y��3=0ƽ�У���a��ֵ��
��2���� ![]() �������ۺ���y=f��x���ĵ����ԣ�
�������ۺ���y=f��x���ĵ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x���ڶ�����[��1��1]���溯������x��[��1��0]ʱ��f��x��=��3x2 ��
��1����x��[0��1]����f��x����
��2��������a��[��1��1]��x��[��1��1]������ʽf��x����2cos2�ȩ�asin��+1����������ȵ�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�е���ѧ������������˲�����������������ǵ��������ݣ������õ�����Ƶ�ʷֲ�ֱ��ͼ��
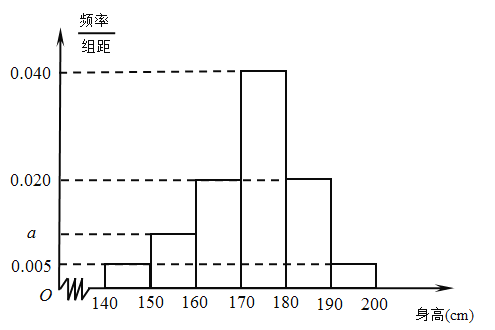
������![]() ��ֵ��
��ֵ��
����������ͬ���е�ÿ�������ø���������е�ֵ���棬���Ƹ�����ѧ���е�ȫ��������ƽ��������
���Ӹ��е���ѧ���������ȡһ������������ֱ��ͼ�е���Ϣ��������������180 cm ���ϵĸ��ʣ�����ȫ����ѧ�������������ڶࣩ�������ȡ![]() �ˣ���
�ˣ���![]() ��ʾ������
��ʾ������![]() ���ϵ��������������������
���ϵ��������������������![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��ż������g��x��=t2x+4��
��ż������g��x��=t2x+4��
��1����a��ֵ��
��2����t=��2ʱ����f��x����g��x���Ľ⼯��
��3��������f��x����ͼ������g��x����ͼ���Ϸ�����ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����fn��x��= ![]() x3��
x3�� ![]() ��n+1��x2+x��n��N*��������{an}����an+1=f'n��an����a1=3��
��n+1��x2+x��n��N*��������{an}����an+1=f'n��an����a1=3��
��1����a2 �� a3 �� a4��
��2�����ݣ�1����������{an}��ͨ�ʽ��������ѧ���ɷ�֤����
��3����֤�� ![]() +
+ ![]() +��+
+��+ ![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����C�IJ��������� ![]() ����Ϊ��������ֱ��l�IJ�������Ϊ
����Ϊ��������ֱ��l�IJ�������Ϊ  ��tΪ��������
��t��������
��1��������C��ֱ��l����ͨ���̣�
��2����ֱ��l������C�ཻ��P��Q���㣬��|PQ|= ![]() ����ʵ��m��ֵ��
����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com