
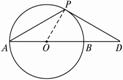
图2-3-8
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
![]()
图2-1-7
A.3 B.6 C.8 D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
某电厂冷却塔外形是如图1-7-8所示的双曲线的一部分绕其中轴(双曲线的虚轴)旋转所成的曲面,其中A,A′是双曲线的顶点,C,C′是冷却塔上口直径的两个端点,B,B′是冷却塔下底直径的两个端点,已知AA′=14 m,CC′=18 m,BB′=22 m,塔高20 m.

图1-7-8
(1)建立坐标系并写出该曲线的方程;
(2)求冷却塔的容积(精确到10 m3,塔壁厚度不计,π取3.14).
查看答案和解析>>
科目:高中数学 来源: 题型:

图2-3-8
查看答案和解析>>
科目:高中数学 来源: 题型:
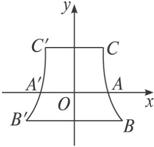
图1-7-8
(1)建立坐标系并写出该曲线的方程;
(2)求冷却塔的容积(精确到10 m3,塔壁厚度不计,π取3.14).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com