练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，AB切⊙O于点B，直线AO交⊙O于D，E两点，BC⊥DE，垂足为C．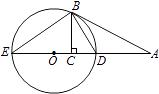

    （1）证明：∠CBD=∠DBA；
    （2）若AD=3DC，BC= ，求⊙O的直径．

    【答案】
    （1）证明：∵DE是⊙O的直径，

    则∠BED+∠EDB=90°，

    ∵BC⊥DE，

    ∴∠CBD+∠EDB=90°，即∠CBD=∠BED，

    ∵AB切⊙O于点B，

    ∴∠DBA=∠BED，即∠CBD=∠DBA；


    （2）证明：由（1）知BD平分∠CBA，

    则 =3，

    ∵BC= ，

    ∴AB=3 ，AC= =4，

    则AD=3，

    由切割线定理得AB2=ADAE，

    即AE= ，

    故DE=AE﹣AD=3，

    即可⊙O的直径为3．


    【解析】（1）根据直径的性质即可证明：∠CBD=∠DBA；（2）结合割线定理进行求解即可求⊙O的直径．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为15.

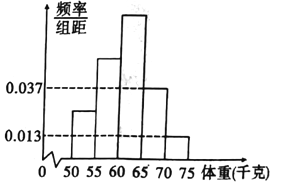
    （1）求该校报考飞行员的总人数；

    （2）以这所学校的样本数据来估计全省的总体数据，若从全省报考飞行员的同学中（人数很多）任选三人，设表示体重超过65公斤的学生人数，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三个数a、b、c∈（0， ），且cosa=a，sin（cosb）=b，cos（sinc）=c，则a、b、c从小到大的顺序是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）若函数在处的切线平行于直线，求实数a的值；

    （Ⅱ）判断函数在区间上零点的个数；

    （Ⅲ）在（Ⅰ）的条件下，若在上存在一点，使得成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（ ）
    A.若l⊥m，mα，则l⊥α
    B.若l⊥α，l∥m，则m⊥α
    C.若l∥α，mα，则l∥m
    D.若l∥α，m∥α，则l∥m

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]，若低于60分的人数是15人，则该班的学生人数是（ ）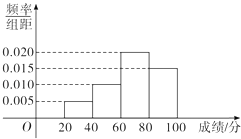

    A.45
    B.50
    C.55
    D.60

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系内，已知A（1，a），B（﹣5，﹣3），C（4，0）；
    （1）当a∈（ ，3）时，求直线AC的倾斜角α的取值范围；
    （2）当a=2时，求△ABC的BC边上的高AH所在直线方程l．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A= ． （Ⅰ）求A∩B，（RB）∪A；
    （Ⅱ）若CA，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数

    （Ⅰ）求不等式的解集；

    （Ⅱ）已知函数的最小值为，若实数且，求的

    最小值．

    查看答案和解析>>

    同步练习册答案