练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数的图象在处的切线过点， .

    （1）若，求函数的极值点；

    （2）设是函数的两个极值点，若，证明： .（提示）

    【答案】（1）或2；（2）见解析

    【解析】试题分析：（1）求导，则.又，曲线在处的切线过点利用斜率相等，可得.，又，可得，则，可得函数的极值点

    （2）由题是方程的两个根，则， ，由，可得， ，∴是函数的极大值， 是函数的极小值，∴要证，只需，计算整理可得 ，令，则，设，利用导数讨论函数

    的性质即可得证

    试题解析;∵，∴.又，曲线在处的切线过点.∴，得.

    （1）∵，∴，令，得，

    解得或2，∴的极值点为或2.

    （2）∵是方程的两个根，∴， ，∵，∴， ，∴是函数的极大值， 是函数的极小值，∴要证，只需， ，令，则，设 ，则，函数在上单调递减，∴，∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设a∈R，解关于x的不等式ax2﹣（a+1）x+1＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设正项数列{an}的前n项和为Sn ， 且满足 ．
    （1）计算a1 ， a2 ， a3的值，并猜想{an}的通项公式；
    （2）用数学归纳法证明{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其导函数的两个零点为和.

    （I）求曲线在点处的切线方程；

    （II）求函数的单调区间；

    （III）求函数在区间上的最值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）是定义在R上的偶函数，f（0）=0，当x＞0时，f（x）=log x．
    （1）求 f（﹣4）的函数值；
    （2）求函数f（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面ABCD是菱形，∠BAD=60°，AB=2，PD= ，O为AC与BD的交点，E为棱PB上一点． （Ⅰ）证明：平面EAC⊥平面PBD；
    （Ⅱ）若PD∥平面EAC，求三棱锥P﹣EAD的体积．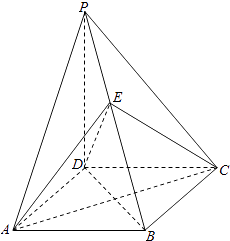

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其导函数的两个零点为和.

    （I）求曲线在点处的切线方程；

    （II）求函数的单调区间；

    （III）求函数在区间上的最值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若曲线在点处的切线斜率为3，且时， 有极值。

    （1）求函数的解析式；

    （2）求函数在上的最值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】经观测，某公路段在某时段内的车流量y（千辆/小时）与汽车的平均速度v（千/小时）之间有函数关系：
    （1）在该时段内，当汽车的平均速度v为多少时车流量y最大？最大车流量为多少？（精确到0.01千辆）；
    （2）为保证在该时段内车流量至少为10千辆/小时，则汽车的平均速度应控制在什么范围内？

    查看答案和解析>>

    同步练习册答案