
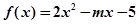 的导函数为
的导函数为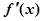 ,若
,若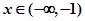 时,
时,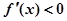 ;
;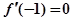 ;
;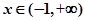 时,
时,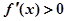 ,则
,则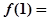 ( )
( )| A.25 | B.17 | C. | D.1 |
科目:高中数学 来源:不详 题型:解答题

 。
。 是函数
是函数 的导数
的导数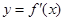 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”; 为常数,若定义在
为常数,若定义在 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称。
对称。 ,请回答下列问题:
,请回答下列问题: 的“拐点”
的“拐点”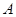 的坐标
的坐标 的图象是否关于“拐点”
的图象是否关于“拐点”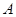 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明) ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
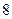 年来生产某种产品的总产量
年来生产某种产品的总产量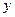 与时间
与时间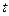 (年)的函数关系如图所示,有下列四种说法:①前三年中产量增长的速度越来越快;②前三年中产量增长的速度越来越慢;③前三年中年产量保持不变;④第三年后,这种产品停止生产。其中正确的说法是 (只要写出说法的序号)
(年)的函数关系如图所示,有下列四种说法:①前三年中产量增长的速度越来越快;②前三年中产量增长的速度越来越慢;③前三年中年产量保持不变;④第三年后,这种产品停止生产。其中正确的说法是 (只要写出说法的序号) 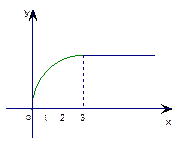
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com