
分析 解出f(x)在[a,+∞)上的零点,对f(x)在各段上零点个数进行讨论,得出a的值.
解答 解:f(x)=$\left\{\begin{array}{l}{2a-x-\frac{4}{x}-3,x∈(-∞,a)}\\{x-\frac{4}{x}-3,x∈[a,+∞)}\end{array}\right.$,
令x-$\frac{4}{x}$-3=0,解得x=-1或x=4.
(1)若a≤-1,则x2=-1,x3=4,
∵2x2=x1+x3,∴x1=-6,
∴x1=-6是方程-x-$\frac{4}{x}$+2a-3=0的解,
∴6+$\frac{2}{3}$+2a-3=0,解得a=-$\frac{11}{6}$.
(2)若-1<a≤4,则x3=4,∴x2=$\frac{{x}_{1}+4}{2}$,且x1,x2为方程-x-$\frac{4}{x}$+2a-3=0的解,
即x1,x2为x2+(3-2a)x+4=0,
∴x1+x2=2a-3,x1x2=4,
解得x1=-2-2$\sqrt{3}$,x2=1-$\sqrt{3}$或x1=-2+2$\sqrt{3}$,x2=1+$\sqrt{3}$.
若x1=-2-2$\sqrt{3}$,x2=1-$\sqrt{3}$,则a=$\frac{{x}_{1}+{x}_{2}+3}{2}$=$\frac{-1-3\sqrt{3}}{2}$,与a>-1矛盾,
若x1=-2+2$\sqrt{3}$,x2=1+$\sqrt{3}$,则a=$\frac{{x}_{1}+{x}_{2}+3}{2}$=$\frac{-1+3\sqrt{3}}{2}$,与x2<a矛盾.
(3)若a>4,则f(x)在[a,+∞)上无零点,而f(x)=0在(-∞,a)上最多只有两解,与f(x)有三个零点矛盾.
综上,a=-$\frac{11}{6}$.
故答案为:-$\frac{11}{6}$
点评 本题考查了分段函数的零点计算,一元二次方程的解法,分类讨论思想,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{65}{9}$,25] | B. | [$\frac{36}{5}$,25] | C. | [16,25] | D. | [9,25] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
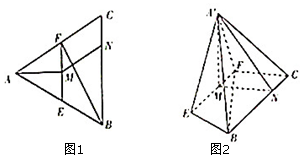 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com