
如图所示,抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1-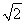 时,切线MA的斜率为-
时,切线MA的斜率为-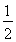 .
.
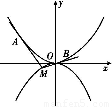
(1)求p的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
(1)2 (2) x2=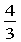 y
y
【解析】
解:(1)因为抛物线C1:x2=4y上任意一点(x,y)的切线斜率为y′=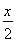 ,且切线MA的斜率为-
,且切线MA的斜率为-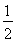 ,
,
所以A点坐标为 .
.
故切线MA的方程为y=-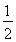 (x+1)+
(x+1)+  .
.
因为点M(1-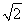 y0)在切线MA及抛物线C2上,于是
y0)在切线MA及抛物线C2上,于是
y0=-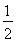 (2-
(2-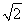 )+
)+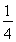 =-
=-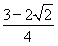 , ①
, ①
y0=-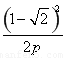 =-
=-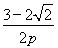 . ②
. ②
由①②得p=2.
(2)设N(x,y),A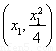 ,B
,B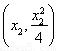 ,
,
x1≠x2,由N为线段AB中点知
x=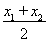 , ③
, ③
y=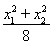 . ④
. ④
切线MA,MB的方程为
y=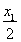 (x-x1)+
(x-x1)+ 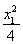 , ⑤
, ⑤
y=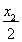 (x-x2)+
(x-x2)+  . ⑥
. ⑥
由⑤⑥得MA,MB的交点M(x0,y0)的坐标为
x0=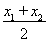 ,y0=
,y0=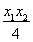 .
.
因为点M(x0,y0)在C2上,
即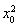 =-4y0,
=-4y0,
所以x1x2=-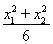 . ⑦
. ⑦
由③④⑦得
x2=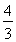 y,x≠0.
y,x≠0.
当x1=x2时,A,B重合于原点O,AB中点N为O,坐标满足x2=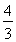 y.
y.
因此AB中点N的轨迹方程为x2=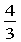 y.
y.


科目:高中数学 来源: 题型:
 如图所示的曲线C是由部分抛物线C 1:y=x2-1(|x|≥1)和曲线C2:x2+
如图所示的曲线C是由部分抛物线C 1:y=x2-1(|x|≥1)和曲线C2:x2+| y2 |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤
(2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤| 3 |
| 2 |
| 9 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.
如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=
如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com