
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在
在![]() 上不具有单调性,求实数m的取值范围;
上不具有单调性,求实数m的取值范围;
(2)若![]() ,
,
①求实数a的值;
②设![]() ,
,![]() ,
,![]() ,当
,当![]() 时,试比较
时,试比较![]() 的大小.
的大小.
【答案】(1) ![]() (2) ①2②t2<t1<t3
(2) ①2②t2<t1<t3
【解析】
试题分析:(1)函数f(x)在(-∞,1]上单调递减,在[1,+∞)上单调递增,因为函数f(x)在[-1,3m]上不单调,以3m>1,解得实数m的取值范围;(2)①因为f(1)=g(1),所以-2+a=0,解得实数a的值;②设![]() ,当x∈(0,1)时,求出三个函数的值域,可得答案
,当x∈(0,1)时,求出三个函数的值域,可得答案
试题解析:(1)因为抛物线y=2x2-4x+a开口向上,对称轴为x=1,
所以函数f(x)在(-∞,1]上单调递减,在[1,+∞)上单调递增,
因为函数f(x)在[-1,3m]上不单调,
所以3m>1,………………………………2分
得![]() ,………………………………3分
,………………………………3分
(2)①因为f(1)=g(1),所以-2+a=0,…………………4分
所以实数a的值为2.……………………………5分
②因为t1=![]() f(x)=x2-2x+1=(x-1)2,
f(x)=x2-2x+1=(x-1)2,
t2=g(x)=log2x,
t3=2x,
所以当x∈(0,1)时,t1∈(0,1),………………………………7分
t2∈(-∞,0),………………………………9分
t3∈(1,2),………………………………11分
所以t2<t1<t3.………………………………12分


科目:高中数学 来源: 题型:
【题目】用系统抽样法从160名学生中抽取容量为20的样本,将160名学生从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,。。。,153~160号).若第15组应抽出的号码为116,则第一组中用抽签方法确定的号码是( )
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 处有极值,求函数
处有极值,求函数![]() 的最大值;
的最大值;
(2)①是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A. 三点确定一个平面 B. 依次首尾相接的四条线段必共面
C. 直线与直线外一点确定一个平面 D. 两条直线确定一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2![]() 的进出口,如图所示,已知旧墙的维修费用为
的进出口,如图所示,已知旧墙的维修费用为![]() 元/
元/![]() ,新墙的造价为
,新墙的造价为![]() 元/
元/![]() ,设利用的旧墙的长度为
,设利用的旧墙的长度为![]() ,费用为
,费用为![]() 元.
元.
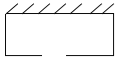
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() 的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
的值,使得修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最少的那份有( )个面包.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
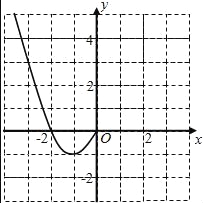
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间;
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com