分析:(1)先证B1O⊥MAC,证明直线与平面垂直,关键要找到两条相交直线与之都垂直.有时候题目中没有现成的直线与直线垂直,需要我们先通过直线与平面垂直去转化一下,如欲证B1O⊥AC,可以先证明AC⊥平面BB1O,从而B1O⊥AM;
(2)以点D为坐标原点,DA为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,根据使B1T⊥平面MAC,建立等式关系,解之即可.
解答:解:(1)证明:∵BB
1⊥平面ABCD,OB⊥AC,
∴B
1O⊥AC.设棱长为2
连接MO、MB
1,则MO=
,B
1O=
,MB
1=3.
∵MO
2+B
1O
2=MB
12,∴∠MOB
1=90°.
∴B
1O⊥MO.
∵MO∩AC=O,∴B
1O⊥平面MAC.
∴B
1O⊥AM;
(2)以点D为坐标原点,DA为x轴,DC为y轴,DD
1为z轴建立空间直角坐标系
A(1,0,0),C(0,1,0),M(0,0,
),B
1(1,1,1)
设点T(0,0,t),则
=(-1,-1,t-1)而
=(-1,1,0),
=(-1,0,)∵使B
1T⊥平面MAC
∴
解得t=-1
∴DT=1时使B
1T⊥平面MAC
点评:证明直线与直线垂直常用的方法有勾股定理、通过直线与平面垂直转化,以及利用空间向量解立体几何等有关知识,属于中档题.

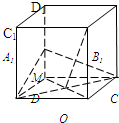 如图,正方体ABCD-A1B1C1D1中,已知O为AC与BD的交点,M为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,已知O为AC与BD的交点,M为DD1的中点.


 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG. 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( ) 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且BF=DE=C1G=C1H=