
 将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为( )
将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为( )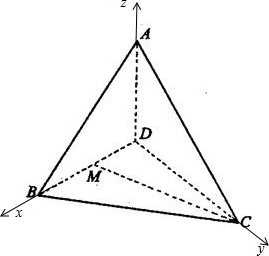 解:设AD=1,则BD=CD=1,AB=AC=
解:设AD=1,则BD=CD=1,AB=AC=| 2 |
| 2 |
| 1 |
| 2 |
| AB |
| CM |
| 1 |
| 2 |
| AB |
| CM |
| ||||
|
|
| ||||||
|
| ||
| 10 |
| ||
| 10 |


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
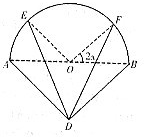 如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<
如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为
将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为



查看答案和解析>>
科目:高中数学 来源:2010年山东省泰安四中高考数学模拟试卷(理科)(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com