
����Ŀ��һ�����д�С��ͬ��4�������2�����������н��ۣ�
�ٴ�����ȡ3��ǡ��һ������ĸ�����![]() ��
��
�ڴ����зŻص�ȡ��6�Σ�ÿ����ȡһ����ȡ����������ķ���Ϊ![]() ��
��
���ִ��в��Żص�ȡ��2�Σ�ÿ����ȡ1�����ڵ�һ��ȡ������������£��ڶ����ٴ�ȡ������ĸ���Ϊ![]() ��
��
�ܴ����зŻص�ȡ��3�Σ�ÿ����ȡһ����������һ��ȡ������ĸ���Ϊ![]() .
.
����������ȷ���۵������________��
���𰸡��٢ڢ�.
��������
�����ݹŵ�����ʹ�ʽ������֪ʶ�ɵý����������ݶ���ֲ��ķ��ʽ�ɵý����
�������������ʽ��м���ɵõ��ڶ����ٴ�ȡ������ĸ����������ݶ����¼��ĸ��ʹ�ʽ�ɵý��.
�ٴ�����ȡ3����ǡ��һ������ĸ�����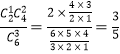 ���ʢ���ȷ��
���ʢ���ȷ��
�������зŻص�ȡ��![]() �Σ�ÿ����ȡһ��
�Σ�ÿ����ȡһ��
ȡ���������![]() ���䷽��Ϊ
���䷽��Ϊ![]() ���ʢ���ȷ��
���ʢ���ȷ��
�����в��Żص�ȡ��![]() ����ÿ����ȡһ�����ڵ�һ��ȡ�������ʱ���л���
����ÿ����ȡһ�����ڵ�һ��ȡ�������ʱ���л���![]() ������
������![]() ��������ڶ����ٴ�ȡ������ĸ���Ϊ
��������ڶ����ٴ�ȡ������ĸ���Ϊ![]() ���ʢ۴���
���ʢ۴���
�������зŻص�ȡ��3����ÿ����ȡһ��ÿ��ȡ������ĸ���Ϊ![]() ��
��
![]() ������һ��ȡ������ĸ���Ϊ
������һ��ȡ������ĸ���Ϊ![]() ���ʢ���ȷ���ʴ�Ϊ�٢ڢ�.
���ʢ���ȷ���ʴ�Ϊ�٢ڢ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�ԲC1��C2�IJ������̷ֱ��� ![]() ����Ϊ��������
����Ϊ�������� ![]() ����Ϊ����������OΪ���㣬x���������Ϊ���Ὠ��������ϵ��
����Ϊ����������OΪ���㣬x���������Ϊ���Ὠ��������ϵ��
��1����ԲC1��C2�ļ����귽�̣�
��2������OM����=a��ԲC1�Ľ���ΪO��P����ԲC2�Ľ���ΪO��Q����|OP||OQ|�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵����һ������Ů�������������У���������ѡ20��Ů����Ϊ�������������ǵ�����(��λ��kg)����õ��������ݰ�������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���з��飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪����������������
���з��飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ����֪����������������![]() �ϵ�Ů����������������
�ϵ�Ů����������������![]() �ϵ�Ů����֮��Ϊ
�ϵ�Ů����֮��Ϊ![]() .
.

(1)��![]() ��ֵ��
��ֵ��
(2)������������������![]() �ϵ�Ů���������ȡ���ˣ�������������
�ϵ�Ů���������ȡ���ˣ�������������![]() �ϵ�Ů��������һ�˱����еĸ���.
�ϵ�Ů��������һ�˱����еĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲC����x��1��2+y2=16��F����1��0����M��ԲC�ϵ�һ�����㣬�߶�MF�Ĵ�ֱƽ�������߶�MC�ཻ�ڵ�P��
�������P�Ĺ켣���̣�
���ǵ�P�Ĺ켣ΪC1 �� A��B��ֱ��x=��2�ϵ����㣬����AF��BF������C1���A��B���������ߣ�����x=��2�����ڵ�Q�����ı���AQBF�����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����
���ڲв�ͼ�У��в��ȽϾ��ȵ�����ˮƽ�Ĵ�״�����ڣ�˵��ѡ�õ�ģ�ͱȽϺ��ʣ��������ָ�����Կ̻��ع��Ч����ֵԽС˵��ģ�͵����Ч��Խ�ã��۱Ƚ�����ģ�͵����Ч�������ԱȽϲв�ƽ���ʹ�С���в�ƽ����ԽС��ģ�����Ч��Խ�ã�����˵����ȷ����(����)
A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������������һ������е÷�Ϊ����������������������������֪�ס�������������ÿ����������еĻ�������6�����Ҽ�����10��9��8��7���ĸ��ʷֱ�Ϊ0.5��3a��a��0.1��������10��9��8���ĸ��ʷֱ�Ϊ0.3��0.3��0.2.
(1)���������ķֲ��У�
(2)������������ѧ�����뷽�������Դ˱Ƚϼס��ҵ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����C�ļ����귽���Ǧ�=1���Լ���Ϊԭ�㣬����Ϊx��������Ὠ��ƽ��ֱ������ϵ��ֱ��l�IJ�������Ϊ  Ϊ��������
��������
��1��д��ֱ��l������C��ֱ�����귽�̣�
��2��������C���������任 ![]() �õ�����C�䣬������C������һ��ΪM��x��y������
�õ�����C�䣬������C������һ��ΪM��x��y������ ![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ���˽�˿͵Ĺ�����Ϣ��������̳��ռ���![]() λ�˿��������������±���
λ�˿��������������±���
һ�ι�����λ��Ԫ�� |
|
|
|
|
|
�˿����� |
|
|
|
|
|
ͳ�ƽ����ʾ![]() λ�˿��й�������
λ�˿��й�������![]() Ԫ�Ĺ˿�ռ
Ԫ�Ĺ˿�ռ![]() �����̳�ÿ�մ�Լ��
�����̳�ÿ�մ�Լ��![]() ���˿ͣ�Ϊ�������̳����۶�ȣ���һ�ι��ﲻ����
���˿ͣ�Ϊ�������̳����۶�ȣ���һ�ι��ﲻ����![]() Ԫ�Ĺ˿ͷ��ż���Ʒ.
Ԫ�Ĺ˿ͷ��ż���Ʒ.
������ȷ��![]() ��
�� ![]() ��ֵ��������ÿ��Ӧ������Ʒ��������
��ֵ��������ÿ��Ӧ������Ʒ��������
��������![]() ��ǰȥ���̳�������ü���Ʒ������
��ǰȥ���̳�������ü���Ʒ������![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����max{m��n}= ![]() ����F��x��y��=max{|x2+2y+2|��|y2��2x+2|}������x��y��R����F��x��y������Сֵ��
����F��x��y��=max{|x2+2y+2|��|y2��2x+2|}������x��y��R����F��x��y������Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com