
分析 考虑到两曲线关于直线y=-x对称,求线段OM的长的最小值,可转化为点P到直线y=-x的最近距离,再利用导数的几何意义,求曲线上斜率为1的切线方程,从而得此距离.
解答 解:∵曲线y=-e-x与y=lnx,其图象关于y=-x对称,
故线段OM的长的最小值,可转化为点P到直线y=-x的最近距离d
设曲线y=-e-x上斜率为1的切线为y=x+b,
∵y′=e-x,由ex=1,得x=0,故切点坐标为(0,-1),即b=-1
∴d=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$
∴线段OM的长的最小值为$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查了函数图象的对称性,导数的几何意义,曲线的切线方程的求法,转化化归的思想方法.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{15}}{15}$,$\frac{1}{3}$) | B. | [$\frac{1}{5}$,$\frac{\sqrt{15}}{15}$) | C. | ($\frac{1}{5}$,$\frac{\sqrt{15}}{15}$] | D. | ($\frac{1}{7}$,$\frac{1}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
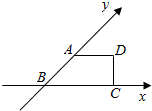 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.
一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 无数个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com