
【题目】在直角坐标系xOy中,直线l的参数方程为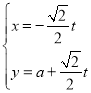 (t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)若直线l过点P(1,1)且与曲线C交于AB两点,求|PA|+|PB|
【答案】(1)l:x+y﹣a=0,C:y2=2x;(2)![]()
【解析】
(1) 消去参数t可得直线l的普通方程,利用极坐标与直角坐标的公式化简求解可得曲线C的直角坐标方程
(2)设直线l的参数方程为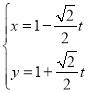 ,再代入抛物线的方程,利用直线参数方程的几何意义求解即可.
,再代入抛物线的方程,利用直线参数方程的几何意义求解即可.
(1)由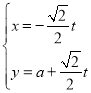 消去参数t可得直线l的普通方程为:x+y﹣a=0,
消去参数t可得直线l的普通方程为:x+y﹣a=0,
由ρsin2θ=2cosθ得ρ2sin2θ=2ρcosθ可得曲线C的直角坐标方程为:y2=2x.
(2)将P(1,1)代入x+y﹣a=0可得a=2,
所以直线l的参数方程为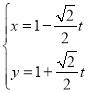 (t为参数)
(t为参数)
将其代入曲线C的普通方程得:t2+4![]() ﹣2=0,设A,B对应的参数为t1,t2,
﹣2=0,设A,B对应的参数为t1,t2,
则t1+t2=﹣4![]() ,t1t2=﹣2<0,∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|=
,t1t2=﹣2<0,∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|=![]() =
=![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点为F且斜率为k的直线l交曲线C于
的焦点为F且斜率为k的直线l交曲线C于![]() 、
、![]() 两点,交圆
两点,交圆![]() 于M,N两点(A,M两点相邻).
于M,N两点(A,M两点相邻).
(1)求证:![]() 为定值;
为定值;
(2)过A,B两点分别作曲线C的切线![]() ,
,![]() ,两切线交于点P,求
,两切线交于点P,求![]() 与
与![]() 面积之积的最小值.
面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积![]() (弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长
(弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长![]() 等于
等于![]() ,其弧所在圆为圆
,其弧所在圆为圆![]() ,若用上述弧田面积计算公式计算得该弧田的面积为
,若用上述弧田面积计算公式计算得该弧田的面积为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() =1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
=1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣3|+|x+2|
(1)求不等式f(x)≤5的解集;
(2)若关于x的不等式f(x)≤a﹣|x|在区间[﹣1,2]上恒成立,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某工厂每天固定成本是4万元,每生产一件产品成本增加100元,工厂每件产品的出厂价定为![]() 元时,生产
元时,生产![]() 件产品的销售收入是
件产品的销售收入是![]() (元),
(元),![]() 为每天生产
为每天生产![]() 件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件
件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件![]() 元进货后又以每件
元进货后又以每件![]() 元销售,
元销售, ![]() ,其中
,其中![]() 为最高限价
为最高限价![]() ,
, ![]() 为销售乐观系数,据市场调查,
为销售乐观系数,据市场调查, ![]() 是由当
是由当![]() 是
是![]() ,
, ![]() 的比例中项时来确定.
的比例中项时来确定.
(1)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 取得最大值?并求
取得最大值?并求![]() 的最大值;
的最大值;
(2)求乐观系数![]() 的值;
的值;
(3)若![]() ,当厂家平均利润最大时,求
,当厂家平均利润最大时,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点.
上的动点.
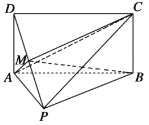
(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积记为
的体积记为![]() ,四棱锥
,四棱锥![]() 的体积记为
的体积记为![]() ,当
,当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com