
| OA |
| 5 |
| OB |
| 5 |
| OA |
| OB |
| OA |
| 5 |
| OB |
| 5 |
| OA |
| OB |
(x+
|
(x-
|
| 5 |
| 5 |
| 5 |
| 5 |
| x2 |
| 9 |
| y2 |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 7π |
| 4 |
| 2 |
| 2 |


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
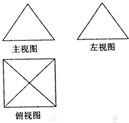 一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )
一个几何体的三视图如图所示,其中主(正)视图是边长为2的正三角形,俯视图是正方形,那么该几何体的左(侧)视图的面积是( )A、2
| ||
B、
| ||
| C、4 | ||
| D、2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| s |
| n |
| A、-2 | ||
B、-
| ||
C、
| ||
D、±
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | m |
 |
| y |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
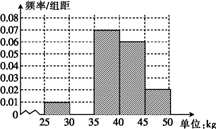 某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).
某养猪厂计划将重量为25kg到50kg的10000头猪向外出售,现从中随机抽取了100头猪进行称重,已知这些猪的重量的频率分布表及不完整的频率分布直方图(如图).| 分组(单位:cm) | 频数 | 频率 |
| [25,30) | 5 | 0.05 |
| [30,35) | ① | 0.20 |
| [35,40) | 35 | ② |
| [40,45) | 30 | 0.30 |
| [45,50] | 10 | 0.10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com