
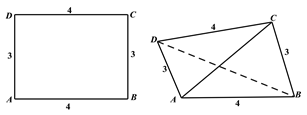
【题目】已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,将其沿对角线
,将其沿对角线![]() 折起,得到四面体
折起,得到四面体![]() ,
,
如图所示,给出下列结论:
①四面体![]() 体积的最大值为
体积的最大值为![]() ;
;
②四面体![]() 外接球的表面积恒为定值;
外接球的表面积恒为定值;
③若![]() 分别为棱
分别为棱![]() 的中点,则恒有
的中点,则恒有![]() 且
且![]() ;
;
④当二面角![]() 为直二面角时,直线
为直二面角时,直线![]() 所成角的余弦值为
所成角的余弦值为![]() ;
;
⑤当二面角![]() 的大小为
的大小为![]() 时,棱
时,棱![]() 的长为
的长为![]() .
.
其中正确的结论有____________________(请写出所有正确结论的序号)
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,
中, ![]() 的参数方程为
的参数方程为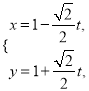 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中, ![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)说明![]() 是哪种曲线,并将
是哪种曲线,并将![]() 的方程化为普通方程;
的方程化为普通方程;
(Ⅱ)![]() 与
与![]() 有两个公共点
有两个公共点![]() ,顶点
,顶点![]() 的极坐标
的极坐标![]() ,求线段
,求线段![]() 的长及定点
的长及定点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,得曲线
轴的正半轴为极轴建立极坐标系,得曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() .
.
(1)化曲线![]() 的参数方程为普通方程,化曲线
的参数方程为普通方程,化曲线![]() 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(2)直线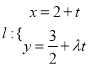 (
(![]() 为参数)过曲线
为参数)过曲线![]() 与
与![]() 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线![]() 平行且与曲线
平行且与曲线![]() 相切的直线方程.
相切的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p1,点数之和大于5的概率记为p2,点数之和为偶数的概率记为p3,则
( )
A. p1<p2<p3 B. p2<p1<p3 C. p1<p3<p2 D. p3<p1<p2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】表示一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系,有人根据函数图象,提出了关于这两个旅行者的如下信息:

①骑自行车者比骑摩托车者早出发3 h,晚到1 h;
②骑自行车者是变速运动,骑摩托车者是匀速运动;
③骑摩托车者在出发1.5 h后追上了骑自行车者;
④骑摩托车者在出发1.5 h后与骑自行车者速度一样.
其中,正确信息的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2-2aln x+(a-2)x,a∈R.
x2-2aln x+(a-2)x,a∈R.
(1)当a=1时,求函数f(x)的图象在点(1,f(1))处的切线方程.
(2)是否存在实数a,对任意的x1,x2∈(0,+∞)且x1≠x2有![]() >a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
>a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数x/个 | 2 | 3 | 4 | 5 |
加工的时间y/h | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
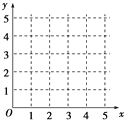
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com