练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．在棱长为1的正方体ABCD-A1B1C1D1中，点P是它的体对角线BD1上一动点，则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$．

    分析 把平面BCD1与平面ABD1沿着BD1展平到一个平面上，连接AC与BD1的交点就是要求的点P的位置，从而求得|AP|+|PC|的最小值．

    解答 解：将平面BCD1与平面ABD1沿着BD1展平到一个平面．然后连接AC与BD1的交点就是要求的点P的位置．
    此时|AP|+|PC|的最小值就是展开后的线段AC的长度，所以所求的值为AC=2×$\frac{1×\sqrt{2}}{\sqrt{3}}$=$\frac{2\sqrt{6}}{3}$，
    故答案为：$\frac{2\sqrt{6}}{3}$．

    点评 本题主要考查直线和平面间的位置关系，把平面BCD1与平面ABD1沿着BD1展平到一个平面上，连接AC与BD1的交点就是要求的点P的位置，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=2x，且f（a）=3，函数g（x）=2ax-$\frac{3}{2}$•9x．
    （1）求常数a的值，并求g（x）的解析式；
    （2）当x∈[-2，1]时，求g（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．圆心在y轴上，半径为5且过点A（3，-4）的圆的方程为x2+y2=25或x2+（y+8）2=25．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知y=$\frac{2x-1}{x-1}$，若x＜0，则y的取值范围是（1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

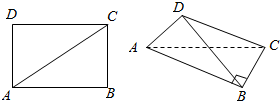    7．如图，在矩形ABCD中，AB=4，BC=3，沿对角线AC把矩形折成二面角D-AC-B，并且D点在平面ABC内的射影落在AB上．
    （1）证明：AD⊥平面DBC；
    （2）求三棱锥D-ABC的体积；
    （3）若在四面体D-ABC内有一球，当球的体积最大时，球的半径是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．如图所示，已知PBD是⊙O的割线，PA、PC是⊙O的切线，A、C为切点，求证：
    （1）PA•AB=PB•AD；
    （2）$\frac{A{D}^{2}}{A{B}^{2}}$=$\frac{PD}{PB}$；
    （3）AD•BC=AB•DC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．（1）已知0＜x＜y＜3，求$\frac{1}{x}+\frac{1}{y-x}+\frac{1}{3-y}$的最小值
    （2）若0＜x＜y＜a，不等式$\frac{1}{x^2}+\frac{1}{{{{（y-x）}^2}}}+\frac{1}{{{{（a-y）}^2}}}$≥9恒成立，求a的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图，⊙O的半径OC垂直于直径AB，M为OB上一点，CM的延长线交⊙O于N，过N点的切线交AB的延长线于P．
    （1）求证：PM2=PB•PA；
    （2）若⊙O的半径为3，OB=$\sqrt{3}$OM，求MN的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．（Ⅰ）求过点（$\sqrt{3}，2\sqrt{2}$）且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程．
    （Ⅱ） 如图所示，A、B是椭圆的两个顶点，C是AB的中点，F为椭圆的右焦点，OC的延长线交椭圆于点M，且|OF|=$\sqrt{2}$，若MF⊥OA，求此椭圆的标准方程．

    查看答案和解析>>

    同步练习册答案