
【题目】已知长方形 ![]() ,
, ![]() ,
, ![]() ,以
,以 ![]() 的中点
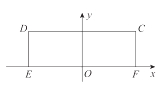
的中点 ![]() 为原点,建立如图所示的平面直角坐标系
为原点,建立如图所示的平面直角坐标系 ![]() .
.
(1)求以 ![]() 为焦点,且过
为焦点,且过 ![]() 两点的椭圆的标准方程;
两点的椭圆的标准方程;
(2)在(1)的条件下,过点 ![]() 作直线
作直线 ![]() 与椭圆交于不同的两点
与椭圆交于不同的两点 ![]() ,设
,设 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,若
,若 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:由题意可得点 ![]() 的坐标分别为
的坐标分别为 ![]() ,
, ![]() ,
, ![]() .设椭圆的标准方程是
.设椭圆的标准方程是 ![]() ,则
,则 ![]() ,∴
,∴ ![]() .∴
.∴ ![]() ,∴椭圆的标准方程为
,∴椭圆的标准方程为 ![]() .
.
(2)解:由题意容易验证直线 ![]() 的斜率不为0,故可设直线
的斜率不为0,故可设直线 ![]() 的方程为
的方程为 ![]() .代入
.代入 ![]() 中,得
中,得 ![]() .设
.设 ![]() ,
, ![]() ,由根与系数关系,得
,由根与系数关系,得 ![]() ①,
①, ![]() ②,∵
②,∵ ![]() ,∴
,∴ ![]() 且
且 ![]() ,将上式①的平方除以②,得
,将上式①的平方除以②,得 ![]() ,即
,即 ![]() ,所以
,所以 ![]() ,由
,由 ![]()
![]() ,即
,即 ![]() .∵
.∵ ![]() ,
, ![]() ,
, ![]() ,又
,又 ![]() ,
, ![]() .故
.故 ![]()
![]()
![]() .令
.令 ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
, ![]() ,
, ![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
, ![]()
【解析】(1)根据题意写出点 E , F , C 的坐标,再结合椭圆的定义求出椭圆的长半轴长a,利用待定系数法写出椭圆方程.
(2)设出直线l的方程代入椭圆方程,结合根与系数关系找到![]() 与A、B点坐标之间的关系,再把
与A、B点坐标之间的关系,再把![]() 用直线方程中的参数表示出来,化归为函数的最值问题求解.
用直线方程中的参数表示出来,化归为函数的最值问题求解.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在无穷数列![]() 中,
中, ![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
, ![]() ,设
,设![]() ,记使得
,记使得![]() 成立的
成立的![]() 的最大值为
的最大值为![]() .
.
(![]() )设数列
)设数列![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,写出
,写出![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )若
)若![]() 为等比例数列,且
为等比例数列,且![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的单调区间;
(2)当k=2时,求证:对于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得当x∈(﹣1,x0)时,恒有f(x)>g(x)成立,试求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下面三个类比结论:①向量 ![]() ,有
,有 ![]() ;类比复数
;类比复数 ![]() ,有
,有 ![]() ;
;
②实数 ![]() 、
、 ![]() 有
有 ![]() ;类比向量
;类比向量 ![]() ,有
,有 ![]() ;
;
③实数 ![]() 、
、 ![]() 有
有 ![]() ,则
,则 ![]() ;类比复数
;类比复数 ![]() ,有
,有 ![]() ,则
,则 ![]() .其中类比结论正确的命题个数为 ( )
.其中类比结论正确的命题个数为 ( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,

(1)证明:PA∥平面EDB
(2)证明:平面BDE![]() 平面PCB
平面PCB
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第 ![]() 个图形包含
个图形包含 ![]() 个小正方形.
个小正方形.
(Ⅰ)求出 ![]() ;
;
(Ⅱ)利用合情推理的“归纳推理思想”归纳出 ![]() 与
与 ![]() 的关系式,并根据你得到的关系式求
的关系式,并根据你得到的关系式求 ![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限分为6个月、12个月、18个月、24个月、36个月五种,对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元,从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计,选取贷款期限的频数如表:
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率.
(Ⅰ)某大学2017年毕业生中共有3人准备申报此项贷款,计算其中恰有两人选择贷款期限为12个月的概率;
(Ⅱ)设给某享受此项政策的自主创业人员补贴为X元,写出X的分布列;该市政府要做预算,若预计2017年全市有600人申报此项贷款,则估计2017年该市共要补贴多少万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com