
分析 (1)利用双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\sqrt{2}$x,且过点$({-\sqrt{2},\sqrt{2}})$,建立方程,求出a,b,即可求双曲线C的标准方程;
(2)设直线l的方程为y-2=k(x-1),即y=kx+2-k,与双曲线方程联立,利用直线l与双曲线C有两个公共点,建立不等式,即可求k的取值范围;
(3)假设存在,设出直线与双曲线的两个交点,代入双曲线方程后利用点差法求斜率,从而得到假设不正确.
解答 解:(1)∵双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\sqrt{2}$x,且过点$({-\sqrt{2},\sqrt{2}})$,
∴$\frac{b}{a}$=$\sqrt{2}$,$\frac{2}{{a}^{2}}-\frac{2}{{b}^{2}}=1$,
∴a=1,b=$\sqrt{2}$,
∴双曲线C的标准方程为${x^2}-\frac{y^2}{2}=1$----------------------------(3分)
(2)设直线l的方程为y-2=k(x-1),即y=kx+2-k,
由$\left\{\begin{array}{l}y=kx+2-k\\ 2{x^2}-{y^2}=2.\end{array}\right.$得(k2-2)x2-2(k2-2k)x+k2-4k+6=0.----------------(5分)
∵直线l与C有两个公共点,
∴得$\left\{\begin{array}{l}{k^2}-2≠0\\△=4{({k^2}-2k)^2}-4({k^2}-2)({k^2}-4k+6)>0.\end{array}\right.$
解之得:k<$\frac{3}{2}$且$k≠±\sqrt{2}$.
∴k的取值范围是$(-∞,-\sqrt{2})∪(-\sqrt{2},\sqrt{2})∪(\sqrt{2},\frac{3}{2})$.-----------------------------(8分)
(3)设以Q(1,1)为中点的弦存在,该直线与双曲线交于M(x1,y1),N(x2,y2)两点
$\left\{\begin{array}{l}2x_1^2-y_1^2=2\\ 2x_2^2-y_2^2=2\end{array}\right.$,作差得kMN=2--------------------------------------------------(11分)
由(2)可知,k=2时,直线l与C没有两个公共点,
∴设以Q(1,1)为中点的弦不存在.----------------------------(12分)
点评 本题是直线与圆锥曲线的综合问题,考查了双曲线的方程,考查判别式法判断直线与圆锥曲线的交点个数,训练了利用点差法求中点弦所在直线的斜率,属中档题.


科目:高中数学 来源: 题型:解答题
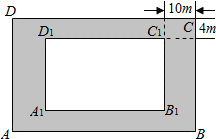 如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m
如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
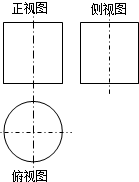 如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{5}{4}π$ | C. | π | D. | $\frac{3}{2}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2-x-2y-$\frac{1}{4}$=0, | B. | x2+y2+x-2y+1=0, | ||
| C. | x2+y2-x+1=0, | D. | x2+y2-x-2y+$\frac{1}{4}$=0, |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
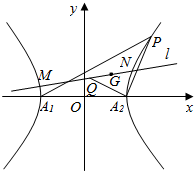 已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.
已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com