
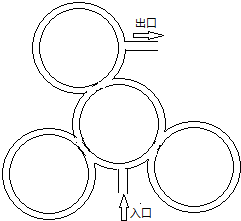
 一人在如图所示景点中的圆环道路上散步.他在交叉路口偏左走的概率为
一人在如图所示景点中的圆环道路上散步.他在交叉路口偏左走的概率为| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 4×3×2 |
| 4×4×4 |
| 6 |
| 16 |
| C | 2 3 |
| 4×3 |
| 4×4×4 |
| 9 |
| 16 |
| 4 |
| 4×4×4 |
| 1 |
| 16 |
| ξ | 0 | 1 | 2 | ||||||
| p |
|
|
|
| 6 |
| 16 |
| 9 |
| 16 |
| 1 |
| 16 |
| 11 |
| 16 |


科目:高中数学 来源:2014届江苏省高二下学期期中考试数学理科试卷(解析版) 题型:解答题
(1) 在直角坐标系xOy中,曲线 的参数方程为
的参数方程为 为参数),M为
为参数),M为 上的动点,P点满足
上的动点,P点满足 ,点P的轨迹为曲线
,点P的轨迹为曲线 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线 与
与 的异于极点的交点为A,与
的异于极点的交点为A,与 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
(2) 某旅游景点给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、-2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内游戏庄家是赢是赔? 通过计算,你得到什么启示?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省达州市高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 ,偏右走的概率为
,偏右走的概率为 (出口处不算交叉路口).
(出口处不算交叉路口).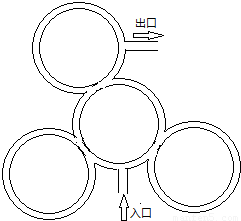
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com