
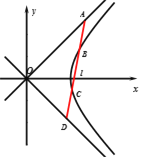
【题目】已知双曲线![]() ,不与
,不与![]() 轴垂直的直线
轴垂直的直线![]() 与双曲线右支交于点
与双曲线右支交于点![]() ,
,![]() ,(
,(![]() 在
在![]() 轴上方,
轴上方,![]() 在
在![]() 轴下方),与双曲线渐近线交于点
轴下方),与双曲线渐近线交于点![]() ,
,![]() (
(![]() 在
在![]() 轴上方),
轴上方),![]() 为坐标原点,下列选项中正确的为( )
为坐标原点,下列选项中正确的为( )
A.![]() 恒成立
恒成立
B.若![]() ,则
,则![]()
C.![]() 面积的最小值为1
面积的最小值为1
D.对每一个确定的![]() ,若
,若![]() ,则
,则![]() 的面积为定值
的面积为定值
【答案】ABD
【解析】
对于A选项,设直线![]() 方程为
方程为![]() ,分别与双曲线方程以及双曲线的渐近线方程联立,求出
,分别与双曲线方程以及双曲线的渐近线方程联立,求出![]() 中点坐标,并判断是否相等即可;对于B选项,由
中点坐标,并判断是否相等即可;对于B选项,由![]() ,得到
,得到![]() ,结合A选项的结果,即可判断选项B是否正确;对于C选项,设直线
,结合A选项的结果,即可判断选项B是否正确;对于C选项,设直线![]() 方程为
方程为![]() ,
,![]() ,直线
,直线![]() 分别与渐近线方程联立,求出
分别与渐近线方程联立,求出![]() 坐标,进而求出
坐标,进而求出![]() 的面积,根据
的面积,根据![]() 的范围,求出
的范围,求出![]() 的面积的范围即可;对于D选项,由已知可得
的面积的范围即可;对于D选项,由已知可得![]() ,利用选项A的方程,得到
,利用选项A的方程,得到![]() 关系,求出
关系,求出![]() 的面积即可.
的面积即可.
设![]() ,代入
,代入![]() 得
得![]() ,①
,①
显然![]() ,
,![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() 是方程①的两个根,
是方程①的两个根,
有![]() ,
,![]() ,
,
设![]() ,
,![]() ,由
,由![]() 得
得![]() ,
,
由![]() ,得
,得![]() ;
;
所以![]() ,所以
,所以![]() 和
和![]() 的中点重合,
的中点重合,
所以![]() ,所以
,所以![]() 恒成立.故A正确.
恒成立.故A正确.
因为![]() 和
和![]() 的中点重合为
的中点重合为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() ,故B正确.
,故B正确.
设直线![]() 方程为
方程为![]() ,
,![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,故C错误.
,故C错误.
因为![]() ,所以
,所以![]() ,得
,得
![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
所以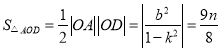 是定值.故D正确.
是定值.故D正确.
故选:ABD.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() 、
、![]() .
.
(1)若![]() ,且函数
,且函数![]() 的图象是函数
的图象是函数![]() 图象的一条切线,求实数
图象的一条切线,求实数![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,函数
,函数![]() 在
在![]() 上总有零点,求实数
上总有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=0,![]() (n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
(n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
A.![]() 是单调递增数列,
是单调递增数列,![]() 是单调递减数列B.
是单调递减数列B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某病毒研究所为了更好地研究“新冠”病毒,计划改建十个实验室,每个实验室的改建费用分为装修费和设备费,每个实验室的装修费都一样,设备费从第一到第十实验室依次构成等比数列,已知第五实验室比第二实验室的改建费用高42万元,第七实验室比第四实验室的改建费用高168万元,并要求每个实验室改建费用不能超过1700万元.则该研究所改建这十个实验室投入的总费用最多需要( )
A.3233万元B.4706万元C.4709万元D.4808万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,以
,以![]() 为圆心过椭圆左顶点
为圆心过椭圆左顶点![]() 的圆与直线
的圆与直线![]() 相切于
相切于![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,问
,问![]() 内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
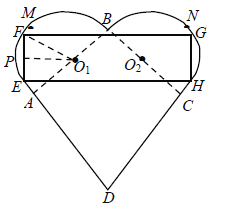
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国法定劳动年龄是![]() 周岁至退休年龄(退休年龄一般指男
周岁至退休年龄(退休年龄一般指男![]() 周岁,女干部身份
周岁,女干部身份![]() 周岁,女工人
周岁,女工人![]() 周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了
周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了![]() 年我国劳动年龄人口和
年我国劳动年龄人口和![]() 周岁人口数量(含预测),得到下表:
周岁人口数量(含预测),得到下表:
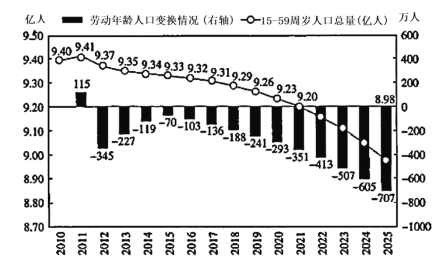
其中![]() 年劳动年龄人口是
年劳动年龄人口是![]() 亿人,则下列结论不正确的是( )
亿人,则下列结论不正确的是( )
A.![]() 年劳动年龄人口比
年劳动年龄人口比![]() 年减少了
年减少了![]() 万人以上
万人以上
B.![]() 这
这![]() 年
年![]() 周岁人口数的平均数是
周岁人口数的平均数是![]() 亿
亿
C.![]() 年,
年,![]() 周岁人口数每年的减少率都小于同年劳动人口每年的减少率
周岁人口数每年的减少率都小于同年劳动人口每年的减少率
D.![]() 年这
年这![]() 年
年![]() 周岁人口数的方差小于这
周岁人口数的方差小于这![]() 年劳动人口数的方差
年劳动人口数的方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com