
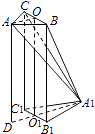
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.
【答案】证明:(Ⅰ)取BC,B1C1的中点为点O,O1 , 连接AO,OO1 , A1O,A1O1 ,
∵AB=AC,∴AO⊥BC
∵平面ABC⊥平面BB1C1C,平面ABC∩平面BB1C1C=BC
∴AO⊥平面BB1C1C
同理A1O1⊥平面BB1C1C,∴AO∥A1O1 , ∴A、O、A1、O1共面
∵OO1⊥BC,AO⊥BC,OO1∩AO=O,∴BC⊥平面OO1A1A
∵AA1平面OO1A1A,∴AA1⊥BC;
(Ⅱ)解:延长A1O1到D,使O1D=OA,则∵O1D∥OA,∴AD∥OO1 , AD=OO1 ,
∵OO1⊥BC,平面A1B1C1⊥平面BB1C1C,平面A1B1C1∩平面BB1C1C=B1C1 ,
∴OO1⊥面A1B1C1 ,
∵AD∥OO1 ,
∴AD⊥面A1B1C1 ,
∵AD=BB1=4,A1D=A1O1+O1D=2+1=3
∴AA1= ![]() =5;
=5;
(Ⅲ)解:∵AO⊥BC,A1O⊥BC,∴∠AOA1是二面角A﹣BC﹣A1的平面角
在直角△OO1A1中,A1O= ![]()
在△OAA1中,cos∠AOA1=﹣ ![]()
∴二面角A﹣BC﹣A1的余弦值为﹣ ![]() .
.
【解析】(Ⅰ)证明AA1⊥BC,只需证明BC⊥平面OO1A1A,取BC,B1C1的中点为点O,O1 , 连接AO,OO1 , A1O,A1O1 , 即可证得;(Ⅱ)延长A1O1到D,使O1D=OA,则可得AD∥OO1 , AD=OO1 , 可证OO1⊥面A1B1C1 , 从而AD⊥面A1B1C1 , 即可求AA1的长;(Ⅲ)证明∠AOA1是二面角A﹣BC﹣A1的平面角,在△OAA1中,利用余弦定理,可求二面角A﹣BC﹣A1的余弦值.
【考点精析】本题主要考查了直线与平面垂直的性质和平面与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行;两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直才能正确解答此题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到数据如表所示(平均每天喝500ml以上为常喝,体重超过50kg为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合计 | 30 |
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
参考数据:
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱A1B1C1D1﹣ABCD中,当底面四边形ABCD满足条件 时,有A1C⊥B1D1 . (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·上海)如图,圆锥的顶点为P,底面的一条直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点. 已知PO=2,OA=1,求三棱锥P-AOC的体积,并求异面直线PA与OE所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点的序列An(xn,0),n∈N*,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,……,An是线段An-2An-1的中点,……
(1)写出xn与xn-1,xn-2之间的关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 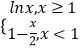 ,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
A.[4﹣2ln2,+∞)
B.( ![]() ,+∞)
,+∞)
C.(﹣∞,4﹣2ln2]
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E= ![]() .
.
(Ⅰ)证明:A1D⊥平面A1BC;
(Ⅱ)求二面角A﹣BD﹣B1的平面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com