
(14分)已知直线L过抛物线x2=2py(p>0)的焦点F,且与抛物线交于A,B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,0是坐标原点
(1)若直线L与x轴平行,且直线与抛物线所围区域的面积为6,求p的值.
(2)过A,B两点分别作该抛物线的切线,两切线相交于N点,求证:![]() ,
,![]()
解析:(1)由条件得![]() M(0,-
M(0,-![]() ),F(0,
),F(0,![]() )把y=
)把y=![]() 代入
代入![]() 中得x=-p或p
中得x=-p或p
所以直线与抛物线所围区域面积S=![]() =
=![]() =
=![]()
又S=6,所以p=3 3分
(2)证:设直线AB的方程为y=kx+![]() ,A(x1,y1),B(x2,y2)
,A(x1,y1),B(x2,y2)
由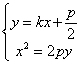 得
得![]() ,
,![]() ,
,![]() ,
,
抛物线方程可化为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以
切线NA的方程为:![]() ,切线NB的方程为:
,切线NB的方程为:![]() ,
,
两方程联立得![]() ,从而可知N点,Q点的横坐标相同,但纵坐标不同,
,从而可知N点,Q点的横坐标相同,但纵坐标不同,
所以![]() ,又
,又![]() ,
,![]() ,所以N(pk,
,所以N(pk,![]() ),而M(0,-
),而M(0,-![]() ),
),
![]() ,又
,又![]() ,
,![]() ,
,![]() 8分
8分
(3)解:因为![]() =
=![]() =
=![]()
=![]() ,又
,又![]() ,
,![]() ,所以k=2或-2
,所以k=2或-2
由于![]() ,
,![]() =
=![]()
![]() ,从而
,从而![]() ,又
,又![]() =
=![]()
![]() ,
,![]() =
=![]() =
=![]()
而![]() 的取值范围是
的取值范围是![]() ,
,![]() ,
,![]() ,而p>0
,而p>0
所以1≤p≤2,又p是不为1的正整数,所以p=2
故抛物线的方程为x2=4y 14分


科目:高中数学 来源: 题型:
|
|
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知直线l与椭圆![]() (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B,![]() ,且
,且![]() ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,![]() 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率![]() ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为![]() ,记
,记![]() ,求
,求![]() 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州八校高三9月期初联考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知直线L: 与抛物线C:
与抛物线C: ,相交于两点
,相交于两点 ,设点
,设点 ,
, 的面积为
的面积为 .
.
(Ⅰ)若直线L上与 连线距离为
连线距离为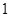 的点至多存在一个,求
的点至多存在一个,求 的范围。
的范围。
(Ⅱ)若直线L上与 连线的距离为
连线的距离为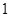 的点有两个,分别记为
的点有两个,分别记为 ,且满足
,且满足 恒成立,求正数
恒成立,求正数 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源:2013届江苏省南通市高二第一学期期末考试数学 题型:解答题
本题满分14分)
已知直线l经过直线3x+4y-2=0与2x+y+2=0的交点P,且垂直于直线x-2y-1=0.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成的三角形的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com