
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,直线
,直线![]() 经过点
经过点![]() .若对任意的实数
.若对任意的实数![]() ,直线
,直线![]() 被圆
被圆![]() 截得的弦长为定值,则直线
截得的弦长为定值,则直线![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.这样的直线不存在
D.这样的直线不存在
科目:高中数学 来源: 题型:
【题目】点E、F、G分别是正方体ABCD-A1B1C1D1的棱AB、BC、B1C1的中点,如图所示,则下列命题中的真命题是________(写出所有真命题的编号).
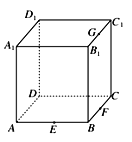
①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形;
②过点F、D1、G的截面是正方形;
③点P在直线FG上运动时,总有AP⊥DE;
④点Q在直线BC1上运动时,三棱锥A-D1QC的体积是定值;
⑤点M是正方体的平面A1B1C1D1内的到点D和C1距离相等的点,则点M的轨迹是一条线段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定直线
到定直线![]() 的距离比到定点
的距离比到定点![]() 的距离大
的距离大![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
, ![]() ,证明以
,证明以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长为定值,并求出此定值.
轴截得的弦长为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)记函数![]() 的图象为曲线
的图象为曲线![]() .设点
.设点![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点.如果在曲线
上的不同两点.如果在曲线![]() 上存在点
上存在点![]() ,使得:①
,使得:①![]() ;②曲线
;②曲线![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() ,则称函数
,则称函数![]() 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数![]() 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)记函数![]() 的图象为曲线
的图象为曲线![]() .设点
.设点![]() ,
,![]() 是曲线
是曲线![]() 上的不同两点.如果在曲线
上的不同两点.如果在曲线![]() 上存在点
上存在点![]() ,使得:①
,使得:①![]() ;②曲线
;②曲线![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() ,则称函数
,则称函数![]() 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数![]() 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,且点
,且点![]() 在直线
在直线![]() 上;
上;
(1)若数列![]() 满足:
满足:![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求
项和,求![]() .
.
(2)是否存在同时满足以下两个条件的三角形?如果存在,求出相应的三角形的三边以及![]() ,
,![]() 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
条件1:三边长是数列![]() 中的连续三项,其中
中的连续三项,其中![]() ;
;
条件2:最小角是最大角的一半.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100个家庭的月均用水量(单位:t),将数据按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成了如图所示的频率分布直方图.
分成5组,制成了如图所示的频率分布直方图.

(1)记事件A:“全市家庭月均用水量不低于6t”,求![]() 的估计值;
的估计值;
(2)假设同组中的每个数据都用该组区间的中点值代替,求全市家庭月均用水量平均数的估计值(精确到0.01);
(3)求全市家庭月均用水量的25%分位数的估计值(精确到0.01).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com