
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,已知sinC+cosC=1-sin![]() .
.
(1)求sinC的值;
(2)若a2+b2=4(a+b)-8,求边c的值.
科目:高中数学 来源: 题型:
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量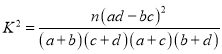 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() ,假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
,假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(1)求甲射击4次,至多1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击,求乙恰好射击5次后被中止射击的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点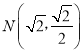 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上午、下午参加“身高与体重”“立定跳远”“肺活量”“握力”“台阶”5个项目的测试,每位同学上午、下午各测试1个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上午、下午都各测试1人,则不同的安排方式有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以![]() ,
,![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,
,![]() ,如此继续下去.有如下结论:
,如此继续下去.有如下结论:

①所作的正三角形的边长构成公比为![]() 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线![]() 上;
上;
③第六个正三角形的不在第五个正三角形边上的顶点![]() 的坐标是
的坐标是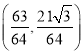 ;
;
④第![]() 个正三角形的不在第
个正三角形的不在第![]() 个正三角形边上的顶点
个正三角形边上的顶点![]() 的横坐标是
的横坐标是![]() ,则
,则![]() .
.
其中正确结论的序号是___________.(把你认为正确结论的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com