
【题目】如图,已知钝角△ABC中,∠B-∠C=90°,∠C=θ,其外接圆⊙O的半径为R.AD是⊙O的一条直径,过点D作⊙O的切线与BC的延长线交于H,过点D作BA的平行线交AC的延长线于E,交过D、O、H的圆于G,联结GH、EH.求△EGH的面积.
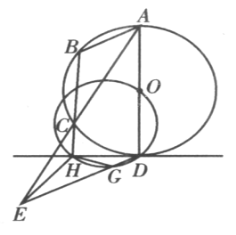
【答案】![]()
【解析】
设直线OH分别交AC、BA的延长线于E’、F.
首先证明:O为线段E’F的中点.
如图,设∠BAC=a,∠CBA=β.联结OB、OC.设∠OAB=x,∠OAC=y,∠OBC=z.
则a+β+θ=180°,x-y=a,x+z=β,z-y=θ.
故x-y+z![]() .
.
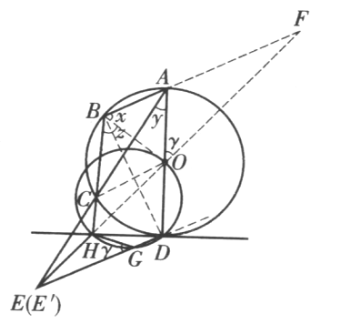
从而,x=90-θ, y=β-90°,z=90°-a.
联结BD,则∠DBH=∠DAC= y,∠BDH=∠DAB=x, BD=2Rsinx.
在△DBH中,由正弦定理得![]() .
.
设∠AOF=γ.在Rt△ODH中,DH=Rtanγ.
所以![]() ,
,
即![]() .
.
则![]()
即 ![]()
在△AOF和△AOE’中,分别用正弦定理可得![]()
所以,OF= OE’.
因为O为线段AD的中点,所以,DE'//BA.则点E’与E重合.于是,∠GEH=∠OED.
又O、D、G、H四点共圆,所以,∠HGE=∠DOH=∠DOE.
因此,△EGH∽△EOD.
过D、O、H的圆的直径![]() . 而∠GDH=90°-x.
. 而∠GDH=90°-x.
在△GDH中,由正弦定理得![]()
故![]() ,即
,即![]() .
.
在△AED中,由正弦定理得![]() .
.
则![]()
由![]() ,得
,得![]() .
.
所以,![]()
![]()
![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】以直角坐标系![]() 的原点为极坐标系的极点,
的原点为极坐标系的极点,![]() 轴的正半轴为极轴.已知曲线
轴的正半轴为极轴.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() ,点
,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的极坐标方程,并化为直角坐标方程;
的极坐标方程,并化为直角坐标方程;
(2)若点![]() ,直线
,直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,当
,当![]() 取最小值时,求直线
取最小值时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用![]() 种不同的颜色给图中的
种不同的颜色给图中的![]() 个格子涂色,每个格子涂一种颜色,要求最多使用
个格子涂色,每个格子涂一种颜色,要求最多使用![]() 种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试问:能否把2008表示成![]() 的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且
的形式?如果可以,这种表示方式是否有无限多个?其中,m、n均为大于100且小于170的正整数,且![]() ;
;![]() 均为两两不相等的小于6的正有理数,且
均为两两不相等的小于6的正有理数,且![]() 均为大于1且小于5的正整数,同时,
均为大于1且小于5的正整数,同时, ![]() 两两不相等,
两两不相等,![]() 也两两不相等请说明理由.
也两两不相等请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线E:y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,
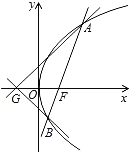
(1)求抛物线E的方程;
(2)已知点G(﹣1,0),延长AF交抛物线E于点B,证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 |
|
|
|
|
|
管理时间 |
|
|
|
|
|
并调查了某村![]() 名村民参与管理的意愿,得到的部分数据如下表所示:
名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 |
|
|
女性村民 |
|
![]() 求出相关系数
求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
![]() 若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取
若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取![]() 人,记取到不愿意参与管理的男性村民的人数为
人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com