
设平面向量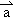 =(
=(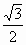 ,-
,- ),
),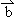 =(
=(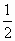 ,
,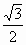 ),若存在不同时为0的两个实数s、t及实数k>0,使
),若存在不同时为0的两个实数s、t及实数k>0,使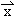 =
=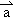 +(t2-k)
+(t2-k)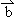 ,
,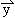 =-s
=-s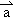 +t
+t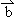 ,且
,且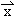 ⊥
⊥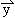 .
.
(1)求函数关系式s=f(t);
(2)若函数s=f(t)在[1,+∞)是单调函数,求证:0<k≤3.
附加题:
(3)设x0≥1,f(x0)≥1,且满足f[f(x0)]=x0,求证f(x0)=x0.
|
(1)∵ ∴| 又 即-s| (2)∵f′(t)=3t2-k f(t)是单调函数 ∴若f(t)是增函数,则f′(t)≥0,恒有3t2≥k,而t∈[1,+∞],∴0<k≤3 若f(t)是减函数,则f′(t)≤0,恒有3t2≤k 而t∈[1,+∞],这样的k不存在,故0<k≤3 (3)设f(x0)=m,由f[f(x0)]=x0,得f(m)=x0 于是 ∴(x0-m)(x02+x0m+m2)(x0-m)(1-k)=0 ∴(x0-m)(x02+m2+x0m+1-k)=0 ∵x0≥1,m=f(x0)≥1∴x02+m2+x0m+1-k≥4-k 而0<k≤3∴x02+m2+x0m+1-k>0,x0=m故f(x0)=x0 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2011届江苏省苏、锡、常、镇四市高三调研测试数学卷(一) 题型:填空题
设平面向量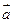 =
=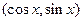 ,
,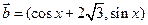 ,
,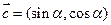 ,
,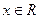 ,
,
⑴若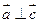 ,求
,求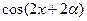 的值;
的值;
⑵若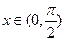 ,证明
,证明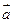 和
和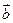 不可能平行;
不可能平行;
⑶若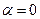 ,求函数
,求函数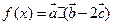 的最大值,并求出相应的
的最大值,并求出相应的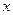 值.
值.
查看答案和解析>>
科目:高中数学 来源:2014届河北冀州中学高一下学期期中理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
设平面向量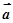 =
( m , -1),
=
( m , -1), 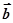 =
( 2 , n ),其中 m, n
=
( 2 , n ),其中 m, n 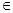 {-2,-1,1,2}.
{-2,-1,1,2}.
(1)记“使得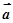 //
//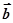 成立的(
m,n )”为事件A,求事件A发生的概率;
成立的(
m,n )”为事件A,求事件A发生的概率;
(2)记“使得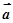 ⊥(
⊥(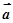 -2
-2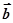 )成立的(
m,n )”为事件B,求事件B发生的概率.
)成立的(
m,n )”为事件B,求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济南市高三下学期二月月考文科数学试卷 题型:解答题
(本小题满分12分)设平面向量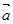 =
( m , 1),
=
( m , 1), 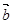 =
( 2 , n ),其中 m, n
=
( 2 , n ),其中 m, n 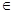 {-2,-1,1,2}.
{-2,-1,1,2}.
(I)记“使得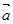 ⊥
⊥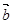 成立的(
m,n )”为事件A,求事件A发生的概率;
成立的(
m,n )”为事件A,求事件A发生的概率;
(II)记“使得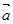 //(
//(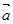 -2
-2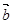 )成立的(
m,n )”为事件B,求事件B发生的概率.
)成立的(
m,n )”为事件B,求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏、锡、常、镇四市高三调研测试数学卷(一) 题型:填空题
设平面向量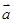 =
=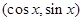 ,
,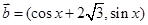 ,
,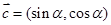 ,
,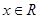 ,
,
⑴若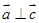 ,求
,求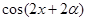 的值;
的值;
⑵若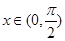 ,证明
,证明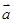 和
和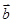 不可能平行;
不可能平行;
⑶若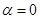 ,求函数
,求函数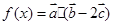 的最大值,并求出相应的
的最大值,并求出相应的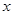 值.
值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com