我国古代数学名著《九章算术》中有如下问题：今有甲乙丙三人持钱，甲语乙丙：各将公等所持钱，半以益我，钱成九十（意思是把你们两个手上的钱各分我一半，我手上就有90钱）；乙复语甲丙，各将公等所持钱，半以益我，钱成七十；丙复语甲乙：各将公等所持钱，半以益我，钱成五十六，则乙手上有（ ）钱.
A. 28 B. 32 C. 56 D. 70
科目：高中数学 来源：2016-2017学年河北省石家庄市高二上学期第三次阶段考试文数试卷（解析版） 题型：选择题
函数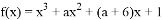
有极大值和极小值，则
的取值范围为（ ）
A. 
B. 
C. 
或
D. 
或
查看答案和解析>>
科目：高中数学 来源：2017届江西省南昌市高三第一次模拟考试数学（理）试卷（解析版） 题型：解答题
已知函数
（
,
是自然对数的底数）.
（1）若
是
上的单调递增函数，求实数
的取值范围；
（2）当
时，证明：函数有最小值，并求函数最小值的取值范围.
查看答案和解析>>
科目：高中数学 来源：2017届江西省南昌市高三第一次模拟考试数学（理）试卷（解析版） 题型：选择题
设某中学的高中女生体重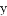
（单位：kg）与身高
（单位：
）具有线性相关关系，根据一组样本数据
（
…，
），用最小二乘法近似得到回归直线方程为
，则下列结论中不正确的是（ ）
A. 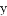与具有正线性相关关系
B. 回归直线过样本的中心点
C. 若该中学某高中女生身高增加1，则其体重约增加0.85
D. 若该中学某高中女生身高为160，则可断定其体重必为50.29.
查看答案和解析>>
科目：高中数学 来源：2016-2017学年福建省漳州市高一上学期期末考试数学试卷（解析版） 题型：解答题
已知某海滨浴场的海浪高度
（单位：米）是时间
（单位：小时，
）的函数，记作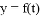
．如表是某日各时的浪高数据：
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
（Ⅰ）在如图的网格中描出所给的点；
（Ⅱ）观察图，从
，
，
中选择一个合适的函数模型，并求出该拟合模型的解析式；
（Ⅲ）依据规定，当海浪高度高于1.25米时才对冲浪爱好者开放，请依据（Ⅱ）的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动．
查看答案和解析>>
科目：高中数学 来源：2017届安徽省合肥市高三第一次教学质量检测数学文试卷（解析版） 题型：选择题
已知双曲线
的两条渐近线分别与抛物线
的准线交于
两点，
为坐标原点．若
的面积为1，则
的值为（ ）
A. 1 B. 
C. 
D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，D为三角形所在平面内一点，且
，则
B. 
C. 
D. 
的夹角为
，
，则
在
上的投影是__________．
