
【题目】某校有微机![]() 台,分别放在
台,分别放在![]() 个房间,各房间开门钥匙互不相同.某期培训班有学员
个房间,各房间开门钥匙互不相同.某期培训班有学员![]() 人(
人(![]() ),每晚恰有
),每晚恰有![]() 人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这
人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这![]() 个学员,使得每晚不论哪
个学员,使得每晚不论哪![]() 个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
【答案】至少应准备![]() 把钥匙分给学员才能满足题目要求
把钥匙分给学员才能满足题目要求
【解析】
注:本题可先设计一个钥匙分配方案,再证明该方案最佳(钥匙总数最少且满足要求).
先将![]() 个房间的
个房间的![]() 把不同钥匙分给某
把不同钥匙分给某![]() 名学员,每人一把(
名学员,每人一把(![]() 个人都可用自己分得的钥匙打开一个房间的门),其余
个人都可用自己分得的钥匙打开一个房间的门),其余![]() 个人,可每人分
个人,可每人分![]() 把(所有房间的钥匙).这批人得的钥匙多,只要那个房间无人,都可开门进去.此方案共需钥匙:
把(所有房间的钥匙).这批人得的钥匙多,只要那个房间无人,都可开门进去.此方案共需钥匙:![]() 把.
把.
下面证明方案最佳.假设钥匙总数![]() ,则由抽屉原理,必有一房里钥匙数
,则由抽屉原理,必有一房里钥匙数![]() .这房间的钥匙最多只能分给
.这房间的钥匙最多只能分给![]() 个学员,因每天只有
个学员,因每天只有![]() 个学员上机房.也恰有
个学员上机房.也恰有![]() 个人不上机房.如果分得这房间钥匙的学员全部不上机房,则这房间的门无法打开,题目条件不能满足.故该方案最佳.即至少应准备
个人不上机房.如果分得这房间钥匙的学员全部不上机房,则这房间的门无法打开,题目条件不能满足.故该方案最佳.即至少应准备![]() 把钥匙分给学员才能满足题目要求.
把钥匙分给学员才能满足题目要求.


科目:高中数学 来源: 题型:
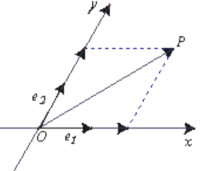
【题目】如图,设![]() 是平面内相交成
是平面内相交成![]() 角的两条数轴 ,
角的两条数轴 ,![]() 分别是
分别是![]() 轴,
轴,![]() 轴正方向同向的单位向量,若向量
轴正方向同向的单位向量,若向量![]() ,则把有序数对
,则把有序数对![]() 叫做向量
叫做向量![]() 在坐标系
在坐标系![]() 中的坐标,假设
中的坐标,假设![]() .
.
(1)计算![]() 的大小;
的大小;
(2)设向量![]() ,若
,若![]() 与
与![]() 共线,求实数
共线,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地沿某条公路行驶一共200公里,遇到红灯个数的概率如下表所示:
红灯个数 | 0 | 1 | 2 | 3 | 4 | 5 | 6个及6个以上 |
概率 | 0.02 | 0.1 |
| 0.35 | 0.2 | 0.1 | 0.03 |
(1)求表中字母![]() 的值;
的值;
(2)求至少遇到4个红灯的概率;
(3)求至多遇到5个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线
分别是双曲线![]() 的左、右焦点,过点
的左、右焦点,过点![]() 作垂直与
作垂直与![]() 轴的直线交双曲线于
轴的直线交双曲线于![]() ,
,![]() 两点,若
两点,若![]() 为锐角三角形,则双曲线的离心率的取值范围是_______.
为锐角三角形,则双曲线的离心率的取值范围是_______.
【答案】![]()
【解析】
根据双曲线的通径求得![]() 点的坐标,将三角形
点的坐标,将三角形![]() 为锐角三角形,转化为
为锐角三角形,转化为![]() ,即
,即![]() ,将表达式转化为含有离心率的不等式,解不等式求得离心率的取值范围.
,将表达式转化为含有离心率的不等式,解不等式求得离心率的取值范围.
根据双曲线的通径可知![]() ,由于三角形
,由于三角形![]() 为锐角三角形,结合双曲线的对称性可知
为锐角三角形,结合双曲线的对称性可知![]() ,故
,故![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() ,故离心率的取值范围是
,故离心率的取值范围是![]() .
.
【点睛】
本小题主要考查双曲线的离心率的取值范围的求法,考查双曲线的通径,考查双曲线的对称性,考查化归与转化的数学思想方法,属于中档题.本小题的主要突破口在将三角形![]() 为锐角三角形,转化为
为锐角三角形,转化为![]() ,利用
,利用![]() 列不等式,再将不等式转化为只含离心率的表达式,解不等式求得双曲线离心率的取值范围.
列不等式,再将不等式转化为只含离心率的表达式,解不等式求得双曲线离心率的取值范围.
【题型】填空题
【结束】
17
【题目】已知命题![]() :方程
:方程![]() 有两个不相等的实数根;命题
有两个不相等的实数根;命题![]() :不等式
:不等式![]() 的解集为
的解集为![]() .若
.若![]() 或
或![]() 为真,
为真,![]() 为假,求实数
为假,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业对设备进行技术升级改造,为了检验改造效果,现从设备改造后生产的大量产品中抽取了100件产品作为样本,检测一项质量指标值,统计整理为如图所示的频率分布直方图:
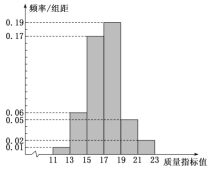
(1)估计该企业所生产产品的质量指标的平均数和中位数(中位数保留一位小数);
(2)若产品的质量指标在![]() 内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在
内,则该产品为残次品,生产并销售一件残次品该企业损失1万元;若产品的质量指标在![]() 范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
范围内,则该产品为特优品,生产一件特优品该企业获利3万元.把样本中的残次品和特优品取出合并在一起,在从中任取2件产品进行销售,那么该企业收入为多少万元的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆M:![]()
![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆![]() 。
。
(1)求椭圆M的方程;
(2)已知![]() ,
,![]() 是椭圆M的下焦点,在椭圆M上是否存在点P,使
是椭圆M的下焦点,在椭圆M上是否存在点P,使![]() 的周长最大?若存在,请求出
的周长最大?若存在,请求出![]() 周长的最大值,并求此时
周长的最大值,并求此时![]() 的面积;若不存在,请说明理由。
的面积;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A,B,P为椭圆C上三点,满足![]() ,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com