[题目]如图.在平面直角坐标系中.Ω是一个与x轴的正半轴.y轴的正半轴分别相切于点C.D的定圆所围成区域.A.B.C.D是该圆的四等分点.若点P满足x≤x′且y≥y′.则称P优于P′.如果Ω中的点Q满足:不存在Ω中的其它点优于Q.那么所有这样的点Q组成的集合是劣弧( ) A.B. C.D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，在平面直角坐标系中，Ω是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域（含边界），A、B、C、D是该圆的四等分点，若点P（x，y）、P′（x′，y′）满足x≤x′且y≥y′，则称P优于P′，如果Ω中的点Q满足：不存在Ω中的其它点优于Q，那么所有这样的点Q组成的集合是劣弧（）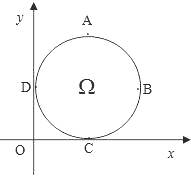
A.
B.
C.
D.

【答案】D
【解析】依题意，在点Q组成的集合中任取一点，过该点分别作平行于两坐标轴的直线，构成的左上方区域与点Q组成的集合无公共元素，这样点Q组成的集合才为所求．故选D．
【考点精析】掌握二元一次不等式（组）所表示的平面区域是解答本题的根本，需要知道不等式组表示的平面区域是各个不等式所表示的平面区域的公共部．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

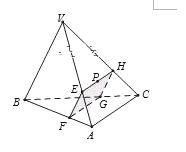
【题目】如图所示，在四面体VABC木块中，P为△VAC的重心，这点P作截面EFGH，若截面EFGH是平行四边形，则该截面把木块分成两部分体积之比为____________．（填体积小与体积大之比）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如果数列a1 ， a2 ， a3 ， … ， an ， …是等差数列，那么下列数列中不是等差数列的是：（）
A.a1+x ， a2+x ， a3+x ， …，an+x ，
B.ka1 ， ka2 ， ka3 ， …，kan ，
C.
D.a1 ， a4 ， a7 ， …a3n﹣2 ，

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

（1）求在上的单调区间；

（2）当时，求不等式的解集；

（3）当时，设函数，求证：不等式在定义域上恒成立.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱锥P-ABC中，PA⊥底面ABC，．点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2．

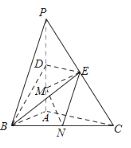
（1）求证：MN∥平面BDE；

（2）求二面角C-EM-N的正弦值；

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某企业生产甲、乙两种产品．已知生产每吨甲产品要用A原料3吨、B原料2吨；生产每吨乙产品要用A原料1吨、B原料3吨．销售每吨甲产品可获得利润5万元、每吨乙产品可获得利润3万元．该企业在一个生产周期内消耗A原料不超过13吨、B原料不超过18吨，那么该企业可获得最大利润是（）
A.12万元
B.20万元
C.25万元
D.27万元

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知集合M={x|3+2x﹣x2＞0}，N={x|x＞a}，若MN，则实数a的取值范围是（）
A.[3，+∞）
B.（3，+∞）
C.（﹣∞，﹣1]
D.（﹣∞，﹣1）