
【题目】有7张卡片分别写有数字![]() 从中任取4张,可排出不同的四位数的个数是__________.
从中任取4张,可排出不同的四位数的个数是__________.
【答案】114
【解析】
根据题意,按取出数字是否重复分4种情况讨论:①、取出的4张卡片中没有重复数字,即取出的4张卡片中的数字为1、2、3、4;②、取出的4张卡片中4有2个重复数字,则2个重复的数字为1或2;③若取出的4张卡片为2张1和2张2;④、取出的4张卡片种有3个重复数字,则重复的数字为1.分别求出每种情况下可以排出四位数的个数,由分类计数原理计算可得答案.
根据题意,分4种情况讨论:
(1)取出的4张卡片中没有重复数字,即取出的4张卡片中的数字为1、2、3、4,此时![]() =24种顺序,可以排出24个四位数;
=24种顺序,可以排出24个四位数;
(2)取出的4张卡片中有2个重复数字,则2个重复的数字为1或2,若重复的数字为1,在2、3、4中取出2个,有![]() 种取法,安排在四个位置中,有
种取法,安排在四个位置中,有![]() 种情况,剩余位置安排数字1,可以排出3×12=36个四位数,同理,若重复的数字为2,也可以排出36个重复数字;
种情况,剩余位置安排数字1,可以排出3×12=36个四位数,同理,若重复的数字为2,也可以排出36个重复数字;
(3)若取出的4张卡片为2张1和2张2,在4个位置安排两个1,有![]() 种情况,剩余位置安排两个2,则可以排出6×1=6个四位数;
种情况,剩余位置安排两个2,则可以排出6×1=6个四位数;
(4)取出的4张卡片中有3个重复数字,则重复的数字为1,在2、3、4中取出1个卡片,有![]() 种取法,安排在四个位置中,有
种取法,安排在四个位置中,有![]() 种情况,剩余位置安排1,可以排出3×4=12个四位数;所以一共有24+36+36+6+12=114个四位数.
种情况,剩余位置安排1,可以排出3×4=12个四位数;所以一共有24+36+36+6+12=114个四位数.
故答案为:114.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为曲线
的极坐标方程为曲线![]() .
.
(Ⅰ)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求直线![]() 和曲线
和曲线![]() 的两个交点到点
的两个交点到点![]() 的距离的和与积.
的距离的和与积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接全国文明城市复检,绵阳某中学组织了本校1000名学生进行社会主义核心价值观、文明常识等内容测试。统计测试成绩数据得到如图所示的频率分布直方图,已知![]() ,满分100分.
,满分100分.
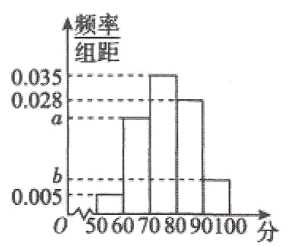
(1)求测试分数在![]() 的学生人数;
的学生人数;
(2)求这1000名学生测试成绩的平均数以及中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 是两个相交平面,则在下列命题中,真命题的序号为( )
是两个相交平面,则在下列命题中,真命题的序号为( )
①若直线![]() ,则在平面
,则在平面![]() 内一定不存在与直线
内一定不存在与直线![]() 平行的直线.
平行的直线.
②若直线![]() ,则在平面
,则在平面![]() 内一定存在无数条直线与直线
内一定存在无数条直线与直线![]() 垂直.
垂直.
③若直线![]() ,则在平面
,则在平面![]() 内不一定存在与直线
内不一定存在与直线![]() 垂直的直线.
垂直的直线.
④若直线![]() ,则在平面
,则在平面![]() 内一定存在与直线
内一定存在与直线![]() 垂直的直线.
垂直的直线.
A. ①③ B. ②③ C. ②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.
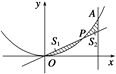
(1)当S1=S2时,求点P的坐标;
(2)当S1+S2有最小值时,求点P的坐标和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有六名同学参加演讲比赛,编号分别为1,2,3,4,5,6,比赛结果设特等奖一名,![]() ,
,![]() ,
,![]() ,
,![]() 四名同学对于谁获得特等奖进行预测.
四名同学对于谁获得特等奖进行预测.![]() 说:不是1号就是2号获得特等奖;
说:不是1号就是2号获得特等奖;![]() 说:3号不可能获得特等奖;
说:3号不可能获得特等奖;![]() 说:4,5,6号不可能获得特等奖;
说:4,5,6号不可能获得特等奖;![]() 说:能获得特等奖的是4,5,6号中的一个.公布的比赛结果表明,
说:能获得特等奖的是4,5,6号中的一个.公布的比赛结果表明,![]() ,
,![]() ,
,![]() ,
,![]() 中只有一个判断正确.根据以上信息,获得特等奖的是( )号同学.
中只有一个判断正确.根据以上信息,获得特等奖的是( )号同学.
A.1B.2C.3D.4,5,6号中的一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 和
和![]() 上的动点,观察直线
上的动点,观察直线![]() 与
与![]() ,
, ![]() 与
与![]() .给出下列结论:
.给出下列结论:
①对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
②对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
③对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() ;
;
④对于任意给定的点![]() ,存在点
,存在点![]() ,使得
,使得![]() .
.
其中正确结论的个数是( ).
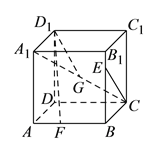
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com